
 如图,抛物线y=ax2+bx-4a经过A(-1,0),C(0,4)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-4a经过A(-1,0),C(0,4)两点,与x轴交于另一点B.分析 (1)将A、C两点的坐标代入解析式中即可求出a与b的值.
(2)根据解析式求出点D的坐标,过点D作DE⊥x轴于点E,求出DE,OE、BE、OC和OE的长度,然后根据梯形面积和三角形面积即可求出答案.
解答 解:(1)将A(-1,0)、C(0,4)代入y=ax2+bx-4a,
∴$\left\{\begin{array}{l}{0=a-b-4a}\\{4=-4a}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$
∴抛物线的解析式为:y=-x2+3x+4
(2)由(1)可知:y=-(x-$\frac{3}{2}$)2+$\frac{25}{4}$
∴D($\frac{3}{2}$,$\frac{25}{4}$),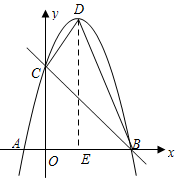
令y=0代入y=-x2+3x+4,
∴x=-1或x=4,
∴B(4,0)
∴DE=$\frac{25}{4}$,AE=$\frac{3}{2}$,BE=$\frac{5}{2}$,OC=4,OE=$\frac{3}{2}$
∴梯形OCDE的面积为:$\frac{1}{2}$(DE+OC)•OE=$\frac{123}{16}$,
△DEB的面积为:$\frac{1}{2}$BE•DE=$\frac{125}{16}$,
∴四边形OCDB的面积为:$\frac{123}{16}$+$\frac{125}{16}$=$\frac{31}{2}$
点评 本题考查二次函数的综合问题,解题的关键是根据条件求出二次函数的解析式,然后求出相关线段的出长度后,根据梯形面积和三角形面积即可求出答案.本题属于中等题型.


科目:初中数学 来源: 题型:解答题
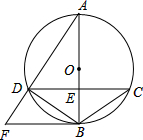 如图,⊙O的直径AB与弦CD交于点E,CE=DE,⊙O的切线BF与弦AD的延长线相交于点F.
如图,⊙O的直径AB与弦CD交于点E,CE=DE,⊙O的切线BF与弦AD的延长线相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 最高气温(℃) | 22 | 23 | 24 | 25 |
| 天数 | 1 | 2 | 2 | 4 |
| A. | 25,24 | B. | 24.5,25 | C. | 24,25 | D. | 23.5,24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
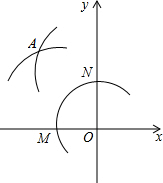 在平面直角坐标系中,在x轴的负半轴与y轴的正半轴上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心、大于$\frac{1}{2}$MN长为半径作弧,两弧在第二象限交于点A,若点A的坐标为($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求点A的坐标.
在平面直角坐标系中,在x轴的负半轴与y轴的正半轴上分别截取OM,ON,使OM=ON;再分别以点M,N为圆心、大于$\frac{1}{2}$MN长为半径作弧,两弧在第二象限交于点A,若点A的坐标为($\frac{m+1}{2}$,$\frac{m+9}{3}$-1),求点A的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )
已知线段AB=4cm,过点B作BC⊥AB,且BC=2cm,连结AC,以C为圆心,CB为半径作弧,交AC于D;以A为圆心,AD为半径作弧,交AB于P,量一量线段AP的长,约为( )| A. | 2cm | B. | 2.5cm | C. | 3cm | D. | 3.5cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com