
【题目】已知:如图,B,C,D三点在![]() 上,
上,![]() ,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
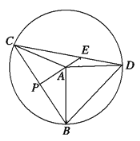
(1)请在图中找出一个与∠CAP相等的角,这个角是 ;
(2)用等式表示线段AC,EC,ED之间的数量关系,并证明.
【答案】(1) ∠BAP;(2)AC,EC,ED满足的数量关系:EC2+ED2=2AC2. 证明见解析.
【解析】
(1)根据等腰三角形ABC三线合一解答即可;
(2)连接EB,由PA是△CAB的垂直平分线,得到EC=EB.,∠ECP=∠EBP,∠ECA=∠EBA. 然后推出∠BAD=∠BED=90°,利用勾股定理可得EB2+ED2=BD2,找到BD2=2AB2,代入可求的EC2+ED2=2AC2的等量关系即可.
(1)∵等腰三角形ABC 且PA是钝角△ABC的高线
∴PA是∠CAB的角平分线
∴∠CAP=∠BAP
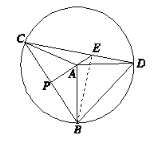
(2)AC,EC,ED满足的数量关系:EC2+ED2=2AC2.
证明:连接EB,与AD交于点F
∵点B,C两点在⊙A上,
∴AC=AB,
∴∠ACP=∠ABP.
∵PA是钝角△ABC的高线,
∴PA是△CAB的垂直平分线.
∵PA的延长线与线段CD交于点E,
∴EC=EB.
∴∠ECP=∠EBP.
∴∠ECP—∠ACP =∠EBP —∠ABP.
即∠ECA=∠EBA.
∵AC=AD,
∴∠ECA=∠EDA
∴∠EBA=∠EDA
∵∠AFB=∠EFD, ∠BCD=45°,
∴∠AFB+∠EBA =∠EFD+∠EDA=90°
即∠BAD=∠BED=90°
∴EB2+ED2=BD2.
∵BD2=AB2+AD2,
∴ BD2=2AB2,
∴EB2+ED2=2AB2,
∴EC2+ED2=2AC2


科目:初中数学 来源: 题型:
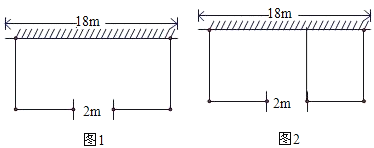
【题目】如图1,若要建一个长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
求:(1)若鸡场面积150平方米,鸡场的长和宽各为多少米?
(2)鸡场面积可能达到200平方米吗?
(3)如图2,若在鸡场内要用竹篱笆加建一道隔栏,则鸡场最大面积可达多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=mx+n与反比例函数y2=![]() (x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点A(a,4)和点B(8,1),与坐标轴分别交于点C和点D.
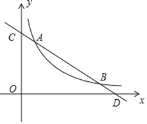
(1)求一次函数与反比例函数的解析式;
(2)观察图象,当x>0时,直接写出y1>y2的解集;
(3)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是半圆的中点,连接CD交OB于点E,点F是AB延长线上一点,CF=EF.
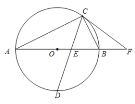
(1)求证:FC是⊙O的切线;
(2)若CF=5,![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京市第十五届人大常委会第十六次会议表决通过《关于修改<北京市生活垃圾管理条例>的决定》,规定将生活垃圾分为厨余垃圾、可回收物、有害垃圾、其它垃圾四大基本品类,修改后的条例将于2020年5月1日实施 .某小区决定在2020年1月到3月期间在小区内设置四种垃圾分类厢:厨余垃圾、可回收物、有害垃圾、其它垃圾,分别记为A、B、C、D,进行垃圾分类试投放,以增强居民垃圾分类意识.
(1)小明家按要求将自家的生活垃圾分成了四类,小明从分好类的垃圾中随机拿了一袋,并随机投入一个垃圾箱中,请用画树状图的方法求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区四类垃圾箱中共1 000千克生活垃圾,数据统计如下(单位:千克):
A | B | C | D | |
厨余垃圾 | 400 | 100 | 40 | 60 |
可回收物 | 25 | 140 | 20 | 15 |
有害垃圾 | 5 | 20 | 60 | 15 |
其它垃圾 | 25 | 15 | 20 | 40 |
求“厨余垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是一张直角三角形纸片,其中
是一张直角三角形纸片,其中![]() ,
,![]() ,小亮将它绕点
,小亮将它绕点![]() 逆时针旋转后
逆时针旋转后![]() 得到
得到![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,当![]() 时,
时,![]() 所在直线与线段
所在直线与线段![]() 有怎样的位置关系?请说明理由.
有怎样的位置关系?请说明理由.
(2)如图2,当![]() ,求
,求![]() 为等腰三角形时的度数.
为等腰三角形时的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
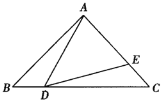
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=1.点D在BC边上(不与B,C点重合),作∠ADE=45°,DE与AC交于点E.
(1)求证:△ABD ∽△DCE;
(2)设BD=x,请用含x的代数式表示AE;
(3)当BD=1时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
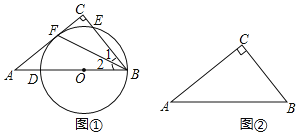
(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com