
| A. | ±$\frac{2\sqrt{3}}{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 将解析式配方成顶点式得对称轴及其顶点纵坐标,作CD⊥AB于点D,由∠BCD=$\frac{1}{2}$∠ACB=60°、tan$∠BCD=\frac{BD}{CD}$,得$\frac{\frac{|b|}{2}}{\frac{{b}^{2}}{4}}$=$\sqrt{3}$,解之可得答案.
解答 解:∵y=-x2+bx=-(x-$\frac{b}{2}$)2+$\frac{{b}^{2}}{4}$,
∴抛物线的对称轴为x=$\frac{b}{2}$,顶点C的纵坐标为$\frac{{b}^{2}}{4}$,
如图,过点C作CD⊥AB于点D,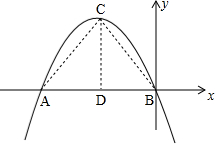
由抛物线对称性知∠ACD=∠BCD=$\frac{1}{2}$∠ACB=60°,
则tan$∠BCD=\frac{BD}{CD}$,即$\frac{\frac{|b|}{2}}{\frac{{b}^{2}}{4}}$=$\sqrt{3}$,
解得:b=0(舍)或b=±$\frac{2\sqrt{3}}{3}$,
故选:A.
点评 本题主要考查二次函数与x轴的交点,熟练掌握二次函数的图象和性质是解题的关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-3)^{2}}$=3 | B. | $\sqrt{36}$=±6 | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | 3+2$\sqrt{3}$=5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
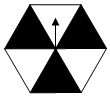 如图上一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影,转动该转盘两次(转动第一次,等转盘完全停止后,再转动第二次,若转盘停止后,指针指向等分线不计入次数),则两次的结果中,指针均落在阴影区域的概率是$\frac{1}{2}$.
如图上一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影,转动该转盘两次(转动第一次,等转盘完全停止后,再转动第二次,若转盘停止后,指针指向等分线不计入次数),则两次的结果中,指针均落在阴影区域的概率是$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
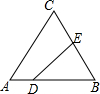 如图,在△ABC中,AC=BC=10,AB=12,D是AB上的一点(不与A、B重合),DE⊥BC,垂足为点E,设BD=x,四边形ACED的周长为y,则下列图象大致反映y与x之间的函数关系的是( )
如图,在△ABC中,AC=BC=10,AB=12,D是AB上的一点(不与A、B重合),DE⊥BC,垂足为点E,设BD=x,四边形ACED的周长为y,则下列图象大致反映y与x之间的函数关系的是( )| A. | 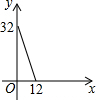 | B. | 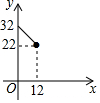 | C. | 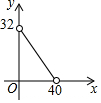 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com