
【题目】问题提出:若一个四边形的两组对边乘积之和等于它的两条对角线的乘积,则称这个四边形为巧妙四边形.
初步思考:(1)写出你所知道的四边形是巧妙四边形的两种图形的名称: , .
(2)小敏对巧妙四边形进行了研究,发现圆的内接四边形一定是巧妙四边形.
如图①,四边形ABCD是⊙O的内接四边形.
求证:AB·CD+BC·AD=AC·BD.
小敏在解答此题时,利用了“相似三角形”进行证明,她的方法如下:
在BD上取点M,使∠MCB=∠DCA.
(请你在下面的空白处完成小敏的证明过程.)
推广运用:如图②,在四边形ABCD中,∠A=∠C=90°,AD=![]() ,AB=
,AB=![]() ,CD=2.求AC的长.
,CD=2.求AC的长.

【答案】(1)正方形,矩形(答案不惟一);(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)根据巧妙四边形的定义可写出符合条件的四边形,等腰梯形,矩形,正方形等,(2)圆内接四边形对角线为圆内两条相交的弦,根据同弧所对圆周角相等可证等角,再根据两角分别对应相等的两个三角形相似可证相似三角形,根据相似三角形的性质可得对应边成比例,即可求证,(3)连接BD,可根据题目条件证明四点共圆,即四边形ABCD为圆内接四边形,再根据(2)的结论代入数值即可计算求解.
试题解析:(1)正方形,矩形(答案不惟一),
(2)∵ 在⊙O中,∠DAC和∠DBC是![]() 所对的圆周角,
所对的圆周角,
∴ ∠DAC=∠DBC,
又 ∠MCB=∠DCA,
∴△MCB∽△DCA,
∴![]() ,
,
即 BC·AD=AC·BM,
∵ 在⊙O中,∠CDB和∠CAB是![]() 所对的圆周角,
所对的圆周角,
∴ ∠CDB=∠CAB.
又 ∠DCM=∠ACB,
∴ △DCM∽△ACB,
∴![]() ,
,
即 AB·CD=AC·DM,
AC·BM=AC·(DM+BM),
即 AB·CD+BC·AD=AC·BD,
(3)连接BD,取BD中点M,连接AM,CM,

在Rt△ABD中,BD=![]() =3,
=3,
在Rt△BCD中,BC=![]() =
=![]() ,
,
∵ 在Rt△ABD中,M是BD中点,
∴AM=![]() BD,
BD,
∵在Rt△BCD中,M是BD中点,
∴CM=![]() BD,
BD,
∴AM=CM=MB=MD,
∴A,B,C,D四点在以点M为圆心,MA为半径的圆上,
即四边形ABCD是⊙O的内接四边形,
由(2)的结论可知AB·CD+BC·AD=AC·BD,
∴ AC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】请在横线上填上合适的内容,完成下面的证明:
如图,射线AH交折线ACGFEN于点B、D、E.已知∠A=∠1,∠C=∠F,BM平分∠CBD,EN平分∠FEH.求证:∠2=∠3.

证明:∵∠A=∠1(已知)
∴AC∥GF( )
∴( )( )
∵∠C=∠F(已知)
∴∠F=∠G
∴( )( )
∴( )( )
∵BM平分∠CBD,EN平分∠FEH
∴∠2= ∠3=
∴∠2=∠3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
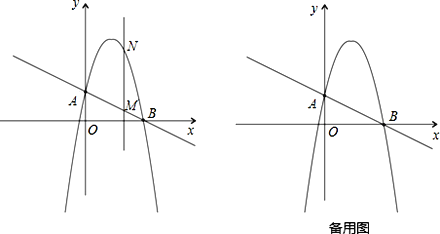
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD,CE分别是AB边上的中线和高.

(1)求证:AE=ED;
(2)若AC=2,求△CDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,
, ![]() .
. ![]() 为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)如果以B,P,N为顶点的三角形与![]() 相似,求点M的坐标.
相似,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A. (﹣3,7) B. (﹣1,7) C. (﹣4,10) D. (0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在⊙O中. AE直径,AD是弦,B为AE延长线上--点,作BC⊥AD,与AD延长线交于点C.且∠CBD=∠A.
(1)判断直线BD与⊙0的位置关系,并证明你的结论;
(2)若∠A=30![]() ,OA=6,求图中阴影部分的面积.
,OA=6,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com