
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.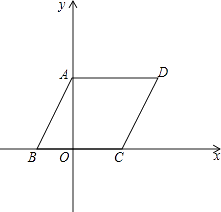
(1)求OA、OB的长.
(2)若点E为x轴正半轴上的点,且S△AOE= ![]() ,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
【答案】
(1)
解:方程x2﹣7x+12=0,
分解因式得:(x﹣3)(x﹣4)=0,
可得:x﹣3=0,x﹣4=0,
解得:x1=3,x2=4,
∵OA>OB,
∴OA=4,OB=3
(2)
解:根据题意,设E(x,0),则S△AOE= ![]() ×OA×x=
×OA×x= ![]() ×4x=
×4x= ![]() ,
,
解得:x= ![]() ,
,
∴E( ![]() ,0),
,0),
∵四边形ABCD是平行四边形,
∴点D的坐标是(6,4),
设经过D、E两点的直线的解析式为y=kx+b,
则 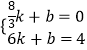 ,
,
解得: 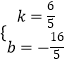 ,
,
∴解析式为y= ![]() x﹣
x﹣ ![]() ;
;
设反比例函数解析式为y= ![]() ,
,
把D(6,4)代入得:m=24,
∴反比例函数解析式为y= ![]() ;
;
在△AOE与△DAO中, ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
又∵∠AOE=∠OAD=90°,
∴△AOE∽△DAO
(3)
解:AO⊥BC,
∴AO平分∠BAC,
分四种情况考虑:
①AC、AF是邻边,点F在射线AB上时,AF=AC=5,
∴点F与B重合,即F(﹣3,0);
②AC、AF是邻边,点F在射线BA上时,M应在直线AD上,且FC垂直平分AM,
此时点F坐标为(3,8);
③AC是对角线时,做AC垂直平分线L,AC解析式为y=﹣ ![]() x+4,直线L过(
x+4,直线L过( ![]() ,2),且k值为
,2),且k值为 ![]() (平面内互相垂直的两条直线k值乘积为﹣1),
(平面内互相垂直的两条直线k值乘积为﹣1),
∴L解析式为y= ![]() x+
x+ ![]() ,
,
联立直线L与直线AB,得: 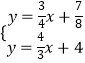 ,
,
解得:x=﹣ ![]() ,y=﹣
,y=﹣ ![]() ,
,
∴F(﹣ ![]() ,﹣
,﹣ ![]() );
);
④AF是对角线时,过C做AB垂线,垂足为N,
∵S△ABC= ![]() BCOA=
BCOA= ![]() ABCN=12,
ABCN=12,
∴CN= ![]() =
= ![]() ,
,
在△BCN中,BC=6,CN= ![]() ,
,
根据勾股定理得BN= ![]() =
= ![]() ,即AN=AB﹣BN=5﹣
,即AN=AB﹣BN=5﹣ ![]() =
= ![]() ,
,
做A关于N的对称点,记为F,AF=2AN= ![]() ,
,
过F做y轴垂线,垂足为G,FG=AFsin∠BAO= ![]() ×
× ![]() =
= ![]() ,
,
∴F(﹣ ![]() ,
, ![]() ),
),
综上所述,满足条件的点有四个:F1(﹣3,0);F2(3,8);F3(﹣ ![]() ,﹣
,﹣ ![]() );F4(﹣
);F4(﹣ ![]() ,
, ![]() ).
).

【解析】(1)解一元二次方程求出OA,OB的长度即可;(2)先根据三角形的面积求出点E的坐标,并根据平行四边形的对边相等的性质求出点D的坐标,然后利用待定系数法求解直线的解析式;分别求出两三角形夹直角的两对应边的比,如果相等,则两三角形相似,否则不相似;(3)根据菱形的性质,分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况,以及AC与AF分别是对角线的情况分别进行求解计算.


科目:初中数学 来源: 题型:
【题目】小李到某城市行政中心大楼办事,假定乘电梯向上一楼记为+1,向下一楼记为–1.
小李从1楼出发,电梯上下楼层依次记录如下(单位:层): +5,–3,+10,–8,+12,–6,–10.
(1)请你通过计算说明小李最后是否回到出发点1楼;
(2)该中心大楼每层高2.8m,电梯每上或下1m需要耗电0.1度.根据小李现在所处的位置,请你算一算,当他办事时电梯需要耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点. 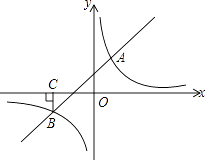
(1)求反比例函数的解析式;
(2)过B点作BC⊥x轴,垂足为C,若P是反比例函数图象上的一点,连接PC,PB,求当△PCB的面积等于5时点P的坐标. 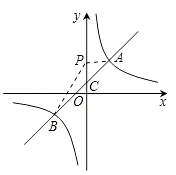
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E. 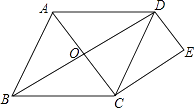
(1)求证:四边形CODE是矩形;
(2)若AB=5,AC=6,求四边形CODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a=![]() ,
,![]() ,c是-27的立方根.
,c是-27的立方根.
(1)b =_______,c =_______;
(2)化简a,并求a+b-c的平方根;
(3)若关于![]() 的不等式组
的不等式组![]() 无解,求
无解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2 017次后形成的图形中所有正方形的面积和是( )
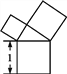
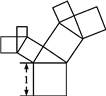
图1 图2
A. 2015 B. 2016 C. 2017 D. 2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强公民的节水意识,合理利用水资源,某市采用价格调控手段来引导市民节约用水:每户居民每月用水不超过15立方米时,按基本价格x元/立方米进行收费;超过15立方米时,加价收费,超过的部分按y元/立方米收费.该市某户居民今年3、4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
3 | 16 | 50 |
4 | 20 | 70 |
5 | m | 不低于36元且不超过95元 |
(1)求x、y的值;
(2)求该居民5月份用水量m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
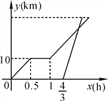
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com