练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列计算正确的是（　　）
    A.a5+a5=a10
    B.﹣a6（﹣a）4=a10
    C.（﹣bc）4÷（﹣bc）2=b2c2
    D.（﹣ab）2a=﹣a3b2

    【答案】C
    【解析】解：A、原式=2a5 ， 错误；
    B、原式=﹣a10 ， 错误；
    C、原式=b2c2 ， 正确；
    D、原式=a3b2 ， 错误，
    故选C
    A、原式合并同类项得到结果，即可做出判断；
    B、原式利用幂的乘方及单项式乘以单项式法则计算得到结果，即可做出判断；
    C、原式利用同底数幂的除法法则计算得到结果，即可做出判断；
    D、原式利用积的乘方运算法则计算得到结果，即可做出判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC，BD交于点O，△AOD是正三角形，AD=4，则平行四边形ABCD的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】①如图1：A、B是两个蓄水池，都在河流a的同侧，为了方便灌溉作物，要在河边建一个抽水站，将河水送到A、B两地，问该站建在河边什么地方，可使所修的渠道最短，试在图中确定该点的位置（保留作图痕迹）．
    ②如图2：某地有两个工厂M、N和两条相交叉的公路a，b现计划修建一座物资仓库，希望仓库到两个工厂的距离相等，到两条公路的距离也相等．你能确定仓库应该建在什么位置吗？在所给的图形中画出你的设计方案．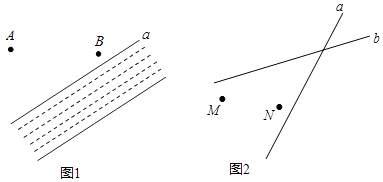

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：2x3﹣8x= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，△ABC的面积是28cm2 ， AB=16cm，AC=12cm，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（　　）

    A.3a+2a=5a2
    B.a2a3=a6
    C.（a+b）（a﹣b）=a2﹣b2
    D.（a+b）2=a2+b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC=50°，∠ADC=30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于E．
    （1）求∠AEC的度数；
    （2）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1 ， CE平分∠ACD1 ， A1E与CE相交于E，∠PAC=50°，∠A1D1C=30°，求∠A1EC的度数．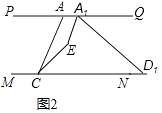
    （3）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（2）相同，求此时∠A1EC的度数．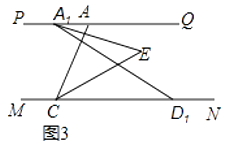

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题正确的是（ ）.

    A.等弧对等弦；B.在同圆中，相等的弦所对的圆周角相等；

    C.平分弦的直径垂直于弦；D.经过切点的直线是圆的切线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

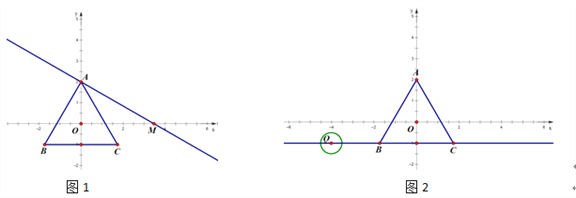
    【题目】设平面内一点到等边三角形中心的距离为d，等边三角形的内切圆半径为r，外接圆半径为R .对于一个点与等边三角形，给出如下定义：满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中，等边△ABC的三个顶点的坐标分别为A(0，2)，B（﹣，﹣1），C(，﹣1).

    （1）已知点D（2，2），E（，1），F（，﹣1）.在D，E，F中，是等边△ABC的中心关联点的是 ；

    （2）如图1，过点A作直线交x轴正半轴于M，使∠AMO=30°.

    ①若线段AM上存在等边△ABC的中心关联点P（m，n），求m的取值范围；

    ②将直线AM向下平移得到直线y=kx+b，当b满足什么条件时，直线y=kx+b上总存在等边△ABC的中心关联点；（直接写出答案，不需过程）

    （3）如图2，点Q为直线y=﹣1上一动点，⊙Q的半径为.当Q从点（﹣4，﹣1）出发，以每秒1个单位的速度向右移动，运动时间为t秒.是否存在某一时刻t，使得⊙Q上所有点都是等边△ABC的中心关联点？如果存在，请直接写出所有符合题意的t的值；如果不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案