
ĄūĖâÄŋĄŋČįÍžĒŲĢŽPΊĄũABCËųÔÚÆ―ÃæÉÏŌŧĩãĢŽĮŌĄÏAPBĢ―ĄÏBPCĢ―ĄÏCPAĢ―120ĄãĢŽÔōĩãP―ÐŨũĄũABCĩÄ·ŅÂíĩãĢŪ
(1)ČįđûĩãPΊČņ―ĮĄũABCĩÄ·ŅÂíĩãĢŽĮŌĄÏABCĢ―60Ąã.
ĒŲĮóÖĪĢš ĄũABPĄŨĄũBCPĢŧ
ĒÚČôPAĢ―3ĢŽPCĢ―4ĢŽĮóPBĩÄģĪĢŧ
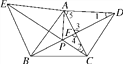
(2)ČįÍžĒÚĢŽŌŅÖŠČņ―ĮĄũABCĢŽ·ÖąðŌÔABĢŽACΊąßÏōÍâŨũÕýĄũABEšÍÕýĄũACDĢŽCEšÍBDÏā―ŧÓÚĩãPĢŽÁŽ―ÓAP.
ĒŲĮóĄÏCPDĩÄķČĘýĢŧ
ĒÚĮóÖĪĢšĩãPΊĄũABCĩÄ·ŅÂíĩãĢŪ

Ąūīð°ļĄŋĢĻ1ĢĐžû―âÎö ĢĻ2ĢĐ60Ąã ĢĻ3ĢĐžû―âÎö
(1)ĒŲÖĪÃũĢšĄßĄÏPABĢŦĄÏPBAĢ―180ĄãĢĄÏAPBĢ―60ĄãĢŽĄÏPBCĢŦĄÏPBAĢ―ĄÏABCĢ―60ĄãĢŽĄāĄÏPABĢ―ĄÏPBC.Ó֥ߥÏAPBĢ―ĄÏBPCĢ―120ĄãĢŽĄāĄũABPĄŨĄũBCP
ĒÚ―âĢšÓÉĒŲŋÉÖŠĄũABPĄŨĄũBCPĢŽĄā ![]() ĢŽĄāPB2Ģ―PAĄĪPCĢ―12ĢŽĄāPBĢ―2
ĢŽĄāPB2Ģ―PAĄĪPCĢ―12ĢŽĄāPBĢ―2![]() .
.
(2)ĒŲ―âĢšČįÍžĢŽĄßĄũABEšÍĄũACDĘĮÕýČý―ĮÐÎĢŽĄāAEĢ―ABĢŽACĢ―ADĢŽĄÏEABĢ―ĄÏ5Ģ―60Ąã.ĄßĄÏEACĢ―ĄÏEABĢŦĄÏBACĢŽĄÏBADĢ―ĄÏBACĢŦĄÏ5ĢŽĄāĄÏEACĢ―ĄÏBADĢŽĄāĄũACEĄÕĄũADBĢŽĄāĄÏ1Ģ―ĄÏ2.ĄßĄÏ3Ģ―ĄÏ4ĢŽĄāĄÏCPDĢ―ĄÏ5Ģ―60Ąã.
ĒÚÖĪÃũĢšÓÉĒŲŋÉÖŠĄÏ1Ģ―ĄÏ2ĢŽĄÏ3Ģ―ĄÏ4ĢŽĄāĄũADFĄŨĄũPCFĢŽĄāAFĄÃPFĢ―DFĄÃCFĢŽĄāAFĄÃDFĢ―PFĄÃCF.ĄßĄÏAFPĢ―ĄÏCFDĢŽĄāĄũAFPĄŨĄũDFCĢŽĄāĄÏAPFĢ―ĄÏACDĢ―60Ąã.ÓÉĒŲŋÉÖŠĄÏCPDĢ―60ĄãĢŽĄāĄÏAPCĢ―ĄÏCPDĢŦĄÏAPFĢ―120ĄãĢŽĄÏBPCĢ―180ĄãĢĄÏCPDĢ―120ĄãĢŽĄāĄÏAPBĢ―360ĄãĢĄÏBPCĢĄÏAPCĢ―120ĄãĢŽĄāĩãPΊĄũABCĩÄ·ŅÂíĩãĢŪ
Ąū―âÎöĄŋĘÔĖâ·ÖÎöĢš ![]() ĒŲÓÉ·ŅÂíĩãĩÄķĻŌåŋÉÖŠĄÏAPBĢ―ĄÏBPCĢ―120ĄãĢŽČŧšóÔŲÖĪÃũĄÏPABĢ―ĄÏPBCžīŋÉÖĪÃũĄũABPĄŨĄũBCP ĒÚÓÉĒŲŋÉÖŠĄũABPĄŨĄũBCPĢŽĩÃĩ―
ĒŲÓÉ·ŅÂíĩãĩÄķĻŌåŋÉÖŠĄÏAPBĢ―ĄÏBPCĢ―120ĄãĢŽČŧšóÔŲÖĪÃũĄÏPABĢ―ĄÏPBCžīŋÉÖĪÃũĄũABPĄŨĄũBCP ĒÚÓÉĒŲŋÉÖŠĄũABPĄŨĄũBCPĢŽĩÃĩ―![]() ĢŽžīŋÉĮóģö
ĢŽžīŋÉĮóģö![]() ĩÄģĪ.
ĩÄģĪ.![]() ČįÍž
ČįÍž![]() ËųĘūĢšĒŲĘŨÏČÖĪÃũĄũACEĄÕĄũADBĢŽÔōĄÏ1Ģ―ĄÏ2ĢŽÓÉĄÏ3Ģ―ĄÏ4ŋÉĩÃĩ―ĄÏCPDĢ―ĄÏ5Ģ―60Ąã.
ËųĘūĢšĒŲĘŨÏČÖĪÃũĄũACEĄÕĄũADBĢŽÔōĄÏ1Ģ―ĄÏ2ĢŽÓÉĄÏ3Ģ―ĄÏ4ŋÉĩÃĩ―ĄÏCPDĢ―ĄÏ5Ģ―60Ąã.
ĒÚÓÉĄÏCPDĢ―60Ąã.ŋÉÖĪÃũĄÏBPCĢ―180ĄãĢĄÏCPDĢ―120ĄãĢŽČŧšóÖĪÃũĄũADFĄŨĄũPCFĢŽÓÉÏāËÆČý―ĮÐÎĩÄÐÔÖĘšÍÅÐķĻķĻĀíÔŲÖĪÃũĄũAFPĄŨĄũDFCĢŽđĘīËŋÉĩÃĩ―ĄÏAPFĢ―ĄÏACDĢ―60ĄãĢŽČŧšóŋÉĮóĩÃĄÏAPCĢ―ĄÏCPDĢŦĄÏAPFĢ―120ĄãĢŽ―ÓÏÂĀīŋÉĮóĩÃĄÏAPBĢ―360ĄãĢĄÏBPCĢĄÏAPCĢ―120Ąã,žīŋÉËĩÃũ.
ĘÔĖâ―âÎöĢš
(1)ĒŲĄßĄÏPABĢŦĄÏPBAĢ―180ĄãĢĄÏAPBĢ―60ĄãĢŽĄÏPBCĢŦĄÏPBAĢ―ĄÏABCĢ―60ĄãĢŽ
ĄāĄÏPABĢ―ĄÏPBC.Ó֥ߥÏAPBĢ―ĄÏBPCĢ―120ĄãĢŽ
ĄāĄũABPĄŨĄũBCP
ĒÚÓÉĒŲŋÉÖŠĄũABPĄŨĄũBCPĢŽ
Ąā![]()
ĄāPB2Ģ―PAĄĪPCĢ―12ĢŽ
![]()
(2)ĒŲČįÍžĢŽĄßĄũABEšÍĄũACDĘĮÕýČý―ĮÐÎĢŽ
ĄāAEĢ―ABĢŽACĢ―ADĢŽĄÏEABĢ―ĄÏ5Ģ―60Ąã.
ĄßĄÏEACĢ―ĄÏEABĢŦĄÏBACĢŽĄÏBADĢ―ĄÏBACĢŦĄÏ5ĢŽ
ĄāĄÏEACĢ―ĄÏBADĢŽ
ĄāĄũACEĄÕĄũADBĢŽ
ĄāĄÏ1Ģ―ĄÏ2.
ĄßĄÏ3Ģ―ĄÏ4ĢŽ
ĄāĄÏCPDĢ―ĄÏ5Ģ―60Ąã.
ĒÚÓÉĒŲŋÉÖŠĄÏ1Ģ―ĄÏ2ĢŽĄÏ3Ģ―ĄÏ4ĢŽ
ĄāĄũADFĄŨĄũPCFĢŽ
ĄāAFĄÃPFĢ―DFĄÃCFĢŽ
ĄāAFĄÃDFĢ―PFĄÃCF.
ĄßĄÏAFPĢ―ĄÏCFDĢŽ
ĄāĄũAFPĄŨĄũDFCĢŽ
ĄāĄÏAPFĢ―ĄÏACDĢ―60Ąã.
ÓÉĒŲŋÉÖŠĄÏCPDĢ―60ĄãĢŽ
ĄāĄÏAPCĢ―ĄÏCPDĢŦĄÏAPFĢ―120ĄãĢŽ
ĄÏBPCĢ―180ĄãĢĄÏCPDĢ―120ĄãĢŽ
ĄāĄÏAPBĢ―360ĄãĢĄÏBPCĢĄÏAPCĢ―120ĄãĢŽ
ĄāĩãPΊĄũABCĩÄ·ŅÂíĩãĢŪ



| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋđÛēėÏÂÁÐ·Ö―âŌōĘ―ĩÄđýģĖĢš
x2+2axĐ3a2
=x2+2ax+a2Đa2Đ3a2ĢĻÏČžÓÉÏa2ĢŽÔŲžõČĨa2ĢĐ
=ĢĻx+aĢĐ2Đ4a2ĢĻÔËÓÃÍęČŦÆ―·―đŦĘ―ĢĐ
=ĢĻx+a+2aĢĐĢĻx+aĐ2a ĢĐĢĻÔËÓÃÆ―·―ēîđŦĘ―ĢĐ
=ĢĻx+3aĢĐĢĻxĐaĢĐ
ÏņÉÏÃæÄĮŅųÍĻđýžÓžõÏîÅäģöÍęČŦÆ―·―Ę―šóÔŲ°ŅķþīÎČýÏîĘ―·Ö―âŌōĘ―ĩÄ·―·ĻĢŽ―ÐŨöÅä·―·ĻĢŪ
ĮëÄãÓÃÅä·―·Ļ·Ö―âŌōĘ―Ģšm2Đ4mn+3n2
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
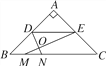
ĄūĖâÄŋĄŋČįÍžĢŽÔÚRtĄũABCÖÐĢŽĄÏAĢ―90ĄãĢŽABĢ―ACĢŽBCĢ―20ĢŽDEĘĮĄũABCĩÄÖÐÎŧÏßĢŽĩãMĘĮąßBCÉÏŌŧĩãĢŽBMĢ―3ĢŽĩãNĘĮÏßķÎMCÉÏĩÄŌŧļöķŊĩãĢŽÁŽ―ÓDNĢŽMEĢŽDNÓëMEÏā―ŧÓÚĩãO.ČôĄũOMNĘĮÖą―ĮČý―ĮÐÎĢŽÔōDOĩÄģĪĘĮ________________ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠŌŧļö―ĮĩÄēđ―ĮĘĮ128Ąã37ĄåÄĮÃīÕâļö―ĮĩÄÓā―ĮĘĮ______________
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŧļöķāÏîĘ―Óëx2Đ2x+1ĩÄšÍĘĮ2xĐ3ĢŽÔōÕâļöķāÏîĘ―ÎŠ ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋžŨĄĒŌŌÁ―ÐĢ·ÖąðÓÐŌŧÄÐŌŧÅŪđē4Ãû―ĖĘĶąĻÃûĩ―ÅĐīåÖÐŅ§Ö§―ĖĢŪ
ĢĻ1ĢĐČôīÓžŨĄĒŌŌÁ―ÐĢąĻÃûĩÄ―ĖĘĶÖÐ·ÖąðËæŧúŅĄ1ÃûĢŽÔōËųŅĄĩÄ2Ãû―ĖĘĶÐÔąðÏāÍŽĩÄļÅÂĘĘĮ ĢŪ
ĢĻ2ĢĐČôīÓąĻÃûĩÄ4Ãû―ĖĘĶÖÐËæŧúŅĄ2ÃûĢŽÓÃÁÐąíŧōŧĘũŨīÍžĩÄ·―·ĻĮóģöÕâ2Ãû―ĖĘĶĀīŨÔÍŽŌŧËųŅ§ÐĢĩÄļÅÂĘĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĮóÏÂÁÐļũĘ―ÖÐxĩÄÖĩĢš
(1)(xĢ2)2Ģ―25Ģŧ (2)Ģ8(1Ģx)3Ģ―27ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋžÆËã(a2b)3ĩÄ―áđûĘĮĢĻ ĢĐ
A. a3bB. a6b3C. a5b3D. a2b3
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔÚŌŧļöČý―ĮÐÎÖÐĢŽļũąßšÍËüËųķÔ―ĮĩÄÕýÏŌĩÄąČÏāĩČĢŪžī![]() ĢŪĀûÓÃÉÏĘö―áÂÛŋÉŌÔĮó―âČįÏÂĖâÄŋĢŪČįĢš
ĢŪĀûÓÃÉÏĘö―áÂÛŋÉŌÔĮó―âČįÏÂĖâÄŋĢŪČįĢš
ÔÚ![]() ÖÐĢŽČôĄÏA=45ĄãĢŽĄÏB=30ĄãĢŽa=6ĢŽĮóbĢŪ
ÖÐĢŽČôĄÏA=45ĄãĢŽĄÏB=30ĄãĢŽa=6ĢŽĮóbĢŪ
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com