
【题目】如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少? 
【答案】解:过点O做OC⊥AB于点D,连接OA.
设半径长为rcm,
∵OC⊥AB,
∴AD= ![]() AB
AB
= ![]() ×8
×8
=4(cm),
∵CD=2cm∴OD=r﹣2(cm)
在Rt△AOD中,由勾股定理得:(r﹣2)2+42=r2
r2﹣4r+4+42=42
4r=20
r=5,
答:该水管的半径是5cm.
【解析】先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD= ![]() AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
【考点精析】通过灵活运用垂径定理的推论,掌握推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等即可以解答此题.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴被折成90°,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2018将与圆周上的数字________重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
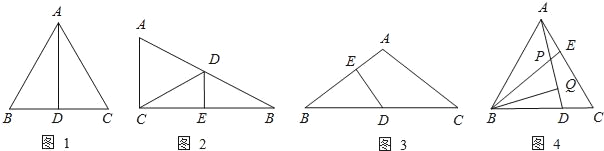
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中, 30°角所对的直角边等于斜边的一半”.
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,△ACD的周长= .
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,那么BE:EA= .
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求BQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,

∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,蚂蚁在5×5的方格(每个小方格的边长均为1 cm)上沿着网格线运动.它从A处出发去寻找B,C,D处的伙伴,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A→D(________,________);D→B(________,________);C→B(________,________).
(2)若蚂蚁的行走路线为A→B→C→D,请计算蚂蚁走过的路程.
(3)若蚂蚁从A处出发去寻找伙伴,它的行走路线依次为(+1,+2),(+3,-1),(-2,+2),请在图中标出这只蚂蚁伙伴的位置E.
(4)在(3)中,若蚂蚁每走1 cm需要消耗1.5焦耳的能量,则蚂蚁在寻找伙伴E的过程中总共需要消耗多少焦耳的能量?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场为了促销,推出两种促销方式:
方式一:所有商品打7.5折销售:
方式二:一次购物满200元送60元现金.
(1)杨老师要购买标价为628元和788元的商品各一件,现有四种购买方案:
方案一:628元和788元的商品均按促销方式①购买;
方案二:628元的商品按促销方式①购买,788元的商品按促销方式②购买;
方案三:628元的商品按促销方式②购买,788元的商品按促销方式①购买;
方案四:628元和788元的商品均按促销方式②购买.
你给杨老师提出的最合理购买方案是 .
![]() (2)通过计算下表中标价在600元到800元之间商品的付款金额,你总结出商品的购买规律是 .
(2)通过计算下表中标价在600元到800元之间商品的付款金额,你总结出商品的购买规律是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com