
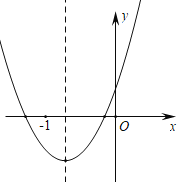
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论:①2a>b;②a﹣b+c>0;③a<b;④a>c,其中正确的结论是( )
A.①③B.②③C.①④D.①③④
【答案】D
【解析】
根据函数图像的位置可以断定a>0,则b>0,而c>0;由对称轴x=﹣![]() >﹣1得2a>b;因为x=-1时,y=a-b+c<0,再由此知a+c<b,所以a<b;综上知道a+c<b<2a,可得a>c.因此此题选D.
>﹣1得2a>b;因为x=-1时,y=a-b+c<0,再由此知a+c<b,所以a<b;综上知道a+c<b<2a,可得a>c.因此此题选D.
解:抛物线的对称轴在y轴右侧,则a、b同号,而a>0,则b>0,而c>0;
①函数的对称性x=﹣![]() >﹣1,故2a>b,故①正确,符合题意;
>﹣1,故2a>b,故①正确,符合题意;
②当x=﹣1时,y=a﹣b+c<0,故②错误,不符合题意;
③由②得,a﹣b+c<0,即a﹣b<﹣c<0,即a<b,故③正确,符合题意;
④由①②得:a﹣b+c<0,即a+c<b<2a,故a>c,故④正确,符合题意;
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
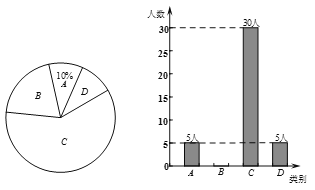
【题目】为了解阳光社区年龄20~60岁居民对垃圾分类的认识,学校课外实践小组随机抽取了该社区、该年龄段的部分居民进行了问卷调查,并将调查数据整理后绘成如下两幅不完整的统计图.图中A表示“全部能分类”,B表示“基本能分类”,C表示“略知一二”,D表示“完全不会”.请根据图中信息解答下列问题:
(1)补全条形统计图并填空:被调查的总人数是 人,扇形图中D部分所对应的圆心角的度数为 ;
(2)若该社区中年龄20~60岁的居民约3000人,请根据上述调查结果,估计该社区中C类有多少人?
(3)根据统计数据,结合生活实际,请你对社区垃圾分类工作提一条合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过原点的直线与反比例函数![]() (k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.
(k>0)的图象交于A,B两点,点A在第一象限点C在x轴正半轴上,连结AC交反比例函数图象于点D.AE为∠BAC的平分线,过点B作AE的垂线,垂足为E,连结DE.若AC=3DC,△ADE的面积为8,则k的值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

查看答案和解析>>
科目:初中数学 来源: 题型:
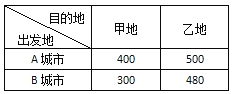
【题目】一方有难,八方支援.已知甲、乙两地急需一批物资,其中甲地需要240吨,乙地需要260吨.A、B两城市通过募捐,很快筹集齐了这种物资,其中A城市筹到物资200吨,B城市筹到物资300吨.已知从A、B两城市将每吨物资分别运往甲、乙两地所需运费成本(单位:元/吨)如表所示.问:怎样调运可使总运费最少?最少运费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,点E,F分别在BC,AD上,BE=DF,连结AE,CF.
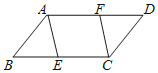
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF为菱形,∠AFC=120°,BE=CE=4,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,在四边形ABCD中,AD//BC,∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止,若E、F分别是AP、BP的中点,设CP=x,△PEF的面积为y,且y与x之间的函数关系的图象如图乙所示,则线段AB长为( )
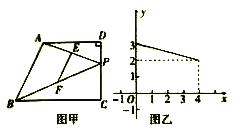
A.2![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 以点
以点![]() 为旋转中心,顺时针旋
为旋转中心,顺时针旋![]() 转,交
转,交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() .直线
.直线![]() 的解析式为:
的解析式为:![]()
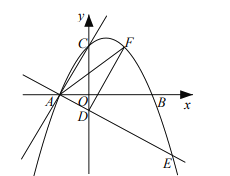
![]() 点
点![]() 是第一象限内抛物线上一点,当
是第一象限内抛物线上一点,当![]() 的面积最大时,在线段
的面积最大时,在线段![]() 上找一点
上找一点![]() (不与
(不与![]() 重合),使
重合),使![]() 的值最小,求出点
的值最小,求出点![]() 的坐标,并直接写出
的坐标,并直接写出![]() 的最小值;
的最小值;
![]() 如图,将
如图,将![]() 沿射线
沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度平移,记平移后的
个单位的速度平移,记平移后的![]() 为
为![]() ,平移时间为
,平移时间为![]() 秒,当
秒,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线G:y=ax2﹣2ax+4(a≠0).
(1)当a=1时,
①抛物线G的对称轴为x= ;
②若在抛物线G上有两点(2,y1),(m,y2),且y2>y1,则m的取值范围是 ;
(2)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段AB恰有一个公共点,结合图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com