
分析 (1)根据分子相同时,分母越大,这个数越小进行判断即可;
(2)根据例题进行计算即可.
解答 解:(1)∵分子相同时,分母越大,这个数越小,
∴$\sqrt{3}-\sqrt{2}$<$\sqrt{2}-\sqrt{1}$;$\sqrt{4}-\sqrt{3}$<$\sqrt{3}-\sqrt{2}$.
(2)$\sqrt{n+1}-\sqrt{n}$<$\sqrt{n}-\sqrt{n-1}$
证明:$\sqrt{n+1}-\sqrt{n}$=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$;$\sqrt{n}-\sqrt{n-1}$=$\frac{1}{\sqrt{n}+\sqrt{n-1}}$;
∵$\frac{1}{\sqrt{n+1}+\sqrt{n}}$$<\frac{1}{\sqrt{n}+\sqrt{n-1}}$,
∴$\sqrt{n+1}-\sqrt{n}$<$\sqrt{n}-\sqrt{n-1}$.
点评 本题主要考查的是比较实数的大小,明确分子相同时,分母越大,这个数越小是解题的关键.


科目:初中数学 来源: 题型:解答题
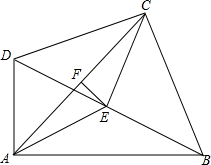 如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点.
如图,在四边形ABCD中,∠DCB=∠DAB=Rt∠,点E是对角线BD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某种细胞经过30分钟由1个分裂成2个.
某种细胞经过30分钟由1个分裂成2个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,图中两个正方形的边长分别是a,b.
如图,图中两个正方形的边长分别是a,b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com