
【题目】如图,马戏团让狮子和公鸡表演跷跷板节目.跷跷板支柱 AB的高度为1.2米.
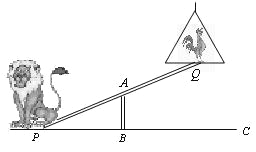
(1)若吊环高度为2米,支点 A为跷跷板 PQ的中点,狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点 A移到跷跷板 PQ的什么位置时,狮子刚好能将公鸡送到吊环上?
【答案】(1)能;(2)支点 A移到跷跷板 PQ的三分之一处.
【解析】试题分析:
(1)如图,过点Q作QH⊥PC于点H,则由题意可得:AB∥QH,从而可得PB:BH=PA:AQ=1,说明AB是△PQH的中位线,则QH=2AB=2.4>2,故狮子能将公鸡送上吊环;
(2)由已知条件易得:△ PAB∽△ PQH,由此可得![]() ,说明当点A移到使AP=
,说明当点A移到使AP=![]() PQ处时,狮子刚好可将公鸡送到吊环上.
PQ处时,狮子刚好可将公鸡送到吊环上.
试题解析:
(1)狮子能将公鸡送到吊环上,理由如下:
如图,过点Q作QH⊥PC于点H,
∵AB⊥PC于点B,
∴AB∥QH,
∴PB:BH=PA:AQ=1,
∴AB是△PQH的中位线,
∴QH=2AB=2.4>2,
∴狮子能将公鸡送到吊环上;
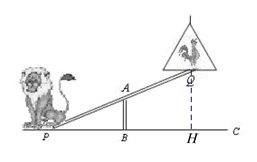
(2)由题意可知:QH=3.6,由(1)可知,AB∥QH,
∴△ PAB∽△ PQH,
∴![]() ,
,
∴PA=![]() PQ,即当点A在PQ上移动到使PA=
PQ,即当点A在PQ上移动到使PA=![]() PQ时,狮子刚好将公鸡送到吊环上.
PQ时,狮子刚好将公鸡送到吊环上.


科目:初中数学 来源: 题型:
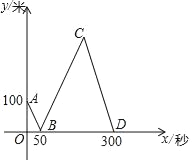
【题目】甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.甲到达目的地时,乙距目的地还有_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() ,点
,点![]() 在
在![]() 轴上,将三角形
轴上,将三角形![]() 沿
沿![]() 轴负方向平移,平移后的图形为三角形
轴负方向平移,平移后的图形为三角形![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
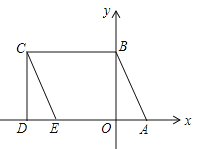
(1)直接写出点![]() 的坐标为 ;
的坐标为 ;
(2)在四边形![]() 中,点
中,点![]() 从点
从点![]() 出发,沿“
出发,沿“![]() ”移动,若点
”移动,若点![]() 的速度为每秒1个单位长度,运动时间为
的速度为每秒1个单位长度,运动时间为![]() 秒,回答下问题:
秒,回答下问题:
①求点![]() 在运动过程中的坐标(用含
在运动过程中的坐标(用含![]() 的式子表示,写出过程);
的式子表示,写出过程);
②当![]() 秒时,点
秒时,点![]() 的横坐标与纵坐标互为相反数;
的横坐标与纵坐标互为相反数;
③当![]() 秒
秒![]() 秒时,设
秒时,设![]() ,
,![]() ,
,![]() ,试问
,试问![]() 之间的数量关系能否确定?若能,请用含
之间的数量关系能否确定?若能,请用含![]() 的式子表式
的式子表式![]() ,写出过程;若不能,说明理由.
,写出过程;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,D为AC的中点,![]() ,则和△AED(不包含△AED)相似的三角形有( )
,则和△AED(不包含△AED)相似的三角形有( )
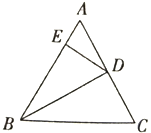
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习三角形的知识时, 发现如下三个有趣的结论:
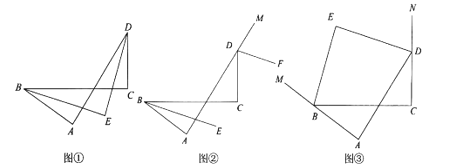
(1)如图①, ∠A=∠C=90°, ∠ABC的平分线与∠ADC的平分线交于点E, 则BE、DE的位置关系是 ;
(2)如图②, ∠A=∠C=90°, BE平分∠ABC, DF平分∠ADC的外角, 则BE与DF的位置关系是 ;
(3)如图③, ∠A=∠C=90°, ∠ABC的外角平分线与∠ADC的外角平分线交于点E, 则BE、DE的位置关系是 . 请你完成命题 (3)证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
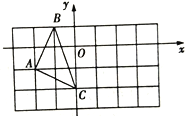
【题目】如图,在平面直角坐标系中,△ABC的三个点坐标分别为A(-2,-1),B(-1,1),C(0,-2).
(1)点B关于坐标原点O对称的点的坐标为____________.
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C1;
(3)以点O为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的相似比为1:2.
查看答案和解析>>
科目:初中数学 来源: 题型:
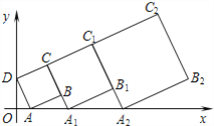
【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,正方形A2018B2018C2018C2017的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
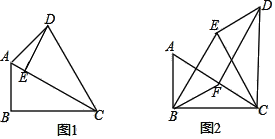
【题目】在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度![]() 得到△DEC,点A、B的对应点分别是D、E.
得到△DEC,点A、B的对应点分别是D、E.
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若![]() =60°时,点F是边AC中点,如图2,求证:DF=BE
=60°时,点F是边AC中点,如图2,求证:DF=BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣2)2x2+(2k+1)x+1=0有实数解,且反比例函数y=![]() 的图象经过第二、四象限,若k是常数,则k的值为( )
的图象经过第二、四象限,若k是常数,则k的值为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com