
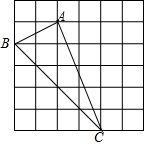
 如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:
如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:分析 (1)利用矩形的面积减去三个顶点上三角形的面积即可;
(2)利用勾股定理求出各边长,进而可得出结论;
(3)根据勾股定理的逆定理即可得出结论.
解答 解:(1)S△ABC=4×5-$\frac{1}{2}$×4×4-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×5=20-8-1-5=6;
(2)∵AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,AC=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$,BC=$\sqrt{{4}^{2}+{4}^{2}}$=$\sqrt{32}$,
∴△ABC的周长=$\sqrt{5}$+$\sqrt{29}$+$\sqrt{32}$;
(3)∵AB=$\sqrt{5}$,AC=$\sqrt{29}$,BC=$\sqrt{32}$,
∴AB2+AC2<BC2,
∴△ABC是钝角三角形.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
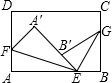 如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?
如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com