
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.

(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
【答案】详见解析.
【解析】试题分析:(1)延长AO交CD延长线于点E,通过证明△AOB≌△EOD可以得到AO=OE,从而证明△ACE为等腰三角形,再利用等腰三角形三线合一性质即可证明CO平分∠ACD;
(2)由第(1)问△AOB≌△EOD可得AB=DE,又因为AC=CE,AC=CD+DE=CD+AB.
试题解析:
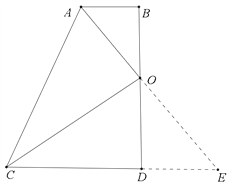
(1)如图,延长AO交CD延长线于点E,
∵O为BD中点,∴BO=DO,
在△AOB和△EOD中, 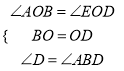 ,
,
∴△AOB≌△EOD,
∴AO=AE,
∵OA⊥OC,
∴AC=CE,
∴CO平分∠ACD;
(2)∵△AOB≌△EOD,
∴AB=DE,
∵AC=CE,CE=CD+DE,
∴AC=CD+DE=CD+AB.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )
A.(﹣2,1)
B.(﹣2,﹣1)
C.(﹣1,﹣2)
D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
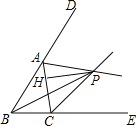
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
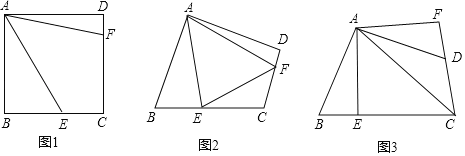
【题目】(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD.
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
(3)如图3,四边形ABCD中,∠BAD≠90°,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F,若BC=8,CD=3,则CE= .(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的对应点位置如图所示 ![]()
(1)用“<”连接0、﹣a、﹣b、﹣1
(2)化简:|a|﹣2|a+b﹣1|﹣ ![]() |b﹣a﹣1|
|b﹣a﹣1|
(3)若a2c+c<0,且c+b>0,求 ![]() +
+ ![]() ﹣
﹣ ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com