
���� ��1�����ݡ�F�任���Ķ�����㼴�ɣ�
��2������F�任���Ķ����г������鼴�ɽ�����⣻
��3��ֻҪ֤��$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$=2���Ƴ���ABC�ס�DEF���ɵ�$\frac{{S}_{��ABC}}{{S}_{��DEF}}$=22���Ƴ�S��ABC=4•S��DEF��
��� �⣺��1��������f��-2��4��=��-1��2����
�ʴ�Ϊ��-1��2����
��2��������$\left\{\begin{array}{l}{1+a=-2}\\{1-b+-1}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$��
��a=1��b=2��
��3����A��x1��y1����b��x2��y2������AB=$\sqrt{��{x}_{1}-{x}_{2}��^{2}+��{y}_{1}-{y}_{2}��^{2}}$��
������D��$\frac{1}{2}$x1+a��$\frac{1}{2}$y1-b����E��$\frac{1}{2}$x2+a��$\frac{1}{2}$y2-b����
��DE=$\sqrt{��\frac{1}{2}{x}_{1}+a-\frac{1}{2}{x}_{2}-a��^{2}+��\frac{1}{2}{y}_{1}-b-\frac{1}{2}{y}_{2}+b��^{2}}$=$\frac{1}{2}$$\sqrt{��{x}_{1}-{x}_{2}��^{2}+��{y}_{1}-{y}_{2}��^{2}}$=$\frac{1}{2}$AB��
ͬ����֤��EF=$\frac{1}{2}$BC��DF=$\frac{1}{2}$AC��
��$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$=2��
���ABC�ס�DEF��
��$\frac{{S}_{��ABC}}{{S}_{��DEF}}$=22��
��S��ABC=4•S��DEF��
�ʴ�ΪS��ABC=4•S��DEF��
���� ���⿼���������ۺ��⣬��F�任���Ķ��塢�������빫ʽ�����������ε��ж������ʵ�֪ʶ������Ĺؼ����������⣬���Ӧ���������빫ʽ������⣬����֤������������������ͻ�Ƶ㣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�о���ֽƬABCD��AB=6��BC=8������ֽƬʹAD��BC�غϵõ��ۺ�EF����ֽƬչƽ����һ���۵�ֽƬ��ʹ��B����EF�ϣ���ʹ�ۺ۾�����A���õ��ۺ�AG����HF=��������
��ͼ�о���ֽƬABCD��AB=6��BC=8������ֽƬʹAD��BC�غϵõ��ۺ�EF����ֽƬչƽ����һ���۵�ֽƬ��ʹ��B����EF�ϣ���ʹ�ۺ۾�����A���õ��ۺ�AG����HF=��������| A�� | 3 | B�� | 4.5 | C�� | 8-3$\sqrt{3}$ | D�� | 8-2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
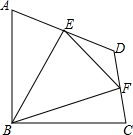 ��ͼ�����ı���ABCD�У���ABC=90�㣬AB=BC=2$\sqrt{2}$��E��F�ֱ���AD��CD���е㣬����BE��BF��EF�����ı���ABCD�����Ϊ6�����BEF�������
��ͼ�����ı���ABCD�У���ABC=90�㣬AB=BC=2$\sqrt{2}$��E��F�ֱ���AD��CD���е㣬����BE��BF��EF�����ı���ABCD�����Ϊ6�����BEF��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+1=0 | B�� | x2+x-1=0 | C�� | x2+2x-3=0 | D�� | 4x2-4x+1=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ֱ�߷ֱ�����ƽ��ֱ��l1��l2��l3���أ���AB=3��BC=6��DE=2����DF�ij�Ϊ��������
��ͼ������ֱ�߷ֱ�����ƽ��ֱ��l1��l2��l3���أ���AB=3��BC=6��DE=2����DF�ij�Ϊ��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com