
分析 (1)根据题目的叙述的方法即可求解;
(2)①把等号右边的式子通分相加,然后根据对应项的系数相等即可求解;
②根据$\frac{1}{n(n+1)(n+2)}$=$\frac{1}{2}$•$\frac{1}{n(n+1)}$-$\frac{1}{2}$•$\frac{1}{(n+1)(n+2)}$把所求的每个分式化成两个分式的差的形式,然后求解.
解答 解:(1)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$;
(2)①∵$\frac{A}{n(n+1)}$+$\frac{B}{(n+1)(n+2)}$
=$\frac{(A+B)n+2A}{n(n+1)(n+2)}$=$\frac{1}{n(n+1)(n+2)}$,
∴$\left\{\begin{array}{l}{A=\frac{1}{2}}\\{A+B=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{A=\frac{1}{2}}\\{B=-\frac{1}{2}}\end{array}\right.$.
∴A和B的值分别是$\frac{1}{2}$和-$\frac{1}{2}$;
②∵$\frac{1}{n(n+1)(n+2)}$=$\frac{1}{2}$•$\frac{1}{n(n+1)}$-$\frac{1}{2}$•$\frac{1}{(n+1)(n+2)}$
=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$)-$\frac{1}{2}$($\frac{1}{n+1}$-$\frac{1}{n+2}$)
∴原式=$\frac{1}{2}$•$\frac{1}{1×2}$-$\frac{1}{2}$•$\frac{1}{2×3}$+$\frac{1}{2}$•$\frac{1}{2×3}$-$\frac{1}{2}$•$\frac{1}{3×4}$+…+$\frac{1}{2}$•$\frac{1}{n(n+1)}$-$\frac{1}{2}$•$\frac{1}{(n+1)(n+2)}$
=$\frac{1}{2}$•$\frac{1}{1×2}$-$\frac{1}{2}$•$\frac{1}{(n+1)(n+2)}$
=$\frac{1}{4}$-$\frac{1}{2(n+1)(n+2)}$
=$\frac{n(n+3)}{4(n+1)(n+2)}$.
点评 本题考查了分式的化简求值,正确理解$\frac{1}{n(n+1)(n+2)}$=$\frac{1}{2}$•$\frac{1}{n(n+1)}$-$\frac{1}{2}$•$\frac{1}{(n+1)(n+2)}$是关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:选择题
| A. | 2x+5=1-x | B. | 3-2(x-1)=7-x | C. | x-2=-2-x | D. | 1-$\frac{1}{4}$x=$\frac{1}{4}$x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解冰箱的使用寿命,采用普查的方式 | |
| B. | 为了了解全国中学生的视力状况,采用普查的方式 | |
| C. | 为了了解人们保护水资源的意识,采用抽样调查的方式 | |
| D. | 对“神舟十一号载人飞船”零部件的检查,采用抽样调查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
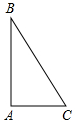 已知:如图在Rt△ABC中,∠BAC=90°.
已知:如图在Rt△ABC中,∠BAC=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com