
| A. | 两条直角边对应相等的两个直角三角形全等 | |
| B. | 一条边和一个锐角对应相等的两个三角形全等 | |
| C. | 有两边和其中一边的对角(此角为钝角)对应相等的两个三角形全等 | |
| D. | 有两条边对应相等的两个直角三角形全等 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
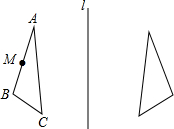 如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:
我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
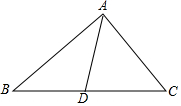 如图,在△ABC中,点D在BC上,在下列四个条件:①∠BAD=∠C;②∠ADC+∠BAC=180°; ③BA2=BD•BC;④$\frac{AB}{AD}$=$\frac{CB}{CA}$中能使△BDA∽△BAC的条件有( )
如图,在△ABC中,点D在BC上,在下列四个条件:①∠BAD=∠C;②∠ADC+∠BAC=180°; ③BA2=BD•BC;④$\frac{AB}{AD}$=$\frac{CB}{CA}$中能使△BDA∽△BAC的条件有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com