Question

（1）如图，在△ABC中，∠ABC、∠ACB的平分线相交于F，过F作DE∥BC，分别交AB、AC于点D、E．判断DE=DB+EC是否成立？为什么？

（2）如图，若点F是∠ABC的平分线和外角∠ACG的平分线的交点，其他条件不变，请猜想线段DE、DB、EC之间有何数量关系？证明你的猜想．

Answer 1

解：（1）成立；
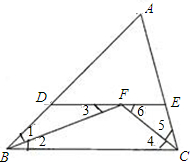
∵△ABC中BF、CF平分∠ABC、∠ACB，
∴∠1=∠2，∠5=∠4．
∵DE∥BC，∴∠2=∠3，∠4=∠6．
∴∠1=∠3，∠6=∠5．
根据在同一个三角形中，等角对等边的性质，可知：BD=DF，EF=CE．
∴DE=DF+EF=BD+CE．
故成立．

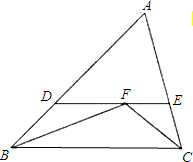
（2）∵BF分∠ABC，
∴∠DBF=∠FBC．
∵DF∥BC，∴∠DFB=∠FBC．
∴∠ABF=∠DFB，
∴BD=DF．
∵CF平分∠ACG，
∴∠ACF=∠FCG．
∵DF∥BC，
∴∠DFC=∠FCG．
∴∠ACF=∠DFC，
∴CE=EF．
∵EF+DE=DF，即DE+EC=BD．
分析：（1）根据平行线的性质和角平分线的性质，解出△BED和△CFD是等腰三角形，通过等量代换即可得出结论．
（2）同（1），只要求出△BDF与△ECF是等腰三角形即可．
点评：本题考查了等腰三角形性质及平行线的性质与角平分线的性质；一般是利用等腰（等边）三角形的性质得出相等的边，进而得出结论是解答本题的基本思路．