
����Ŀ������ABC�У�AB=AC����F��BC�ӳ�����һ�㣬��CFΪ�ߣ�������CDEF��ʹ����CDEF���A��BC��ͬ�࣬����BE����G��BE���е㣬����AG��DG��
��1����ͼ�٣�����BAC=��DCF=90��ʱ��ֱ��д��AG��DG��λ�ú�������ϵ��
��2����ͼ�ڣ�����BAC=��DCF=60��ʱ����̽��AG��DG��λ�ú�������ϵ��
��3������BAC=��DCF=��ʱ��ֱ��д��AG��DG��������ϵ��

���𰸡�(1) AG��DG��AG=DG;(2) AG��DG��AG=DG��֤�������������3��DG=AGtan![]() .
.
��������
�����������1���ӳ�DG��BC����H������AH��AD��ͨ��֤����BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤����ABH�ա�ACD���ó���BAH=��CAD��AH=AD�����������HAD=90�㣬�������AG��GD��AG=GD��
��2���ӳ�DG��BC����H������AH��AD��ͨ��֤����BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤����ABH�ա�ACD���ó���BAH=��CAD��AH=AD�����������HAD�ǵȱ������Σ�����֤��AG��GD��AG=![]() DG��
DG��
��3���ӳ�DG��BC����H������AH��AD��ͨ��֤����BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤����ABH�ա�ACD���ó���BAH=��CAD��AH=AD�����������HAD�ǵ��������Σ�����֤��DG=AGtan![]() ��
��
�����������1��AG��DG��AG=DG��
֤�����ӳ�DG��BC����H������AH��AD��
���ı���CDEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
����BGH����EGD��

���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣬
�ߡ�DCF=90�㣬
���DCB=90�㣬
���ACD=45�㣬
���ABH=��ACD=45�㣬
����ABH����ACD��

���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
�ߡ�BAH+��HAC=90�㣬
���CAD+��HAC=90�㣬����HAD=90�㣬
��AG��GD��AG=GD��
��2��AG��GD��AG=![]() DG��
DG��
֤�����ӳ�DG��BC����H������AH��AD��
���ı���CDEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
����BGH����EGD��

���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=��DCF=60�㣬
���ABC=60�㣬��ACD=60�㣬
���ABC=��ACD=60�㣬
����ABH����ACD��

���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
���BAC=��HAD=60�㣻
��AG��HD����HAG=��DAG=30�㣬
��tan��DAG=tan30��=![]() ��
��
��AG=![]() DG��
DG��
��3��DG=AGtan![]() ��
��
֤�����ӳ�DG��BC����H������AH��AD��
���ı���CDEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
����BGH����EGD��

���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=��DCF=����
���ABC=90�㩁![]() ����ACD=90�㩁
����ACD=90�㩁![]() ��
��
���ABC=��ACD��
����ABH����ACD��

���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
���BAC=��HAD=����
��AG��HD����HAG=��DAG=![]() ��
��
��tan��DAG=tan![]() =
=![]() ��
��
��DG=AGtan![]() ��
��



 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��һ��ֱ�ǣ�������OC���ٷֱ�����AOC�͡�BOC��ƽ����OD��OE��
��1����ͼ�٣�����BOC��70��ʱ�����DOE�Ķ�����
��2����ͼ�ڣ�������OC�ڡ�AOB����O����תʱ����DOE�Ĵ�С�Ƿ����仯���仯��˵�����ɣ������䣬���DOE�Ķ�����
��3����ͼ�ۣ�������OC�ڡ�AOB����O����תʱ������ͼ�Σ��жϡ�DOE�Ĵ�С�Ƿ����仯���仯��˵�����ɣ������䣬���DOE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��������jiong���ǽ�ʱ�������������һ���������Ƶ����飮��ͼ��ʾ��һ�ű߳�Ϊ20�������ε�ֽƬ����ȥ����һ����Сֱ�������κ�һ�������εõ�һ����������ͼ������Ӱ���֣������ȥ��С�����γ��Ϳ��ֱ�Ϊx��y����ȥ������Сֱ�������ε���ֱ�DZ߳�Ҳ�ֱ�Ϊx��y��
��1���ú���x��y�Ĵ���ʽ��ʾ��ͼ���������������
��2����![]() ʱ�����ʱ�������������
ʱ�����ʱ�������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����нǶȲ������Ƕ�����ڽǺ͵���(����)
A.270��B.360��C.540��D.900��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʦ������һ��ѧ����������Զ�ɼ�����¼���£���λ��m����2.00��2.11��2.35��2.15��2.20��2.17����ô�������ݵ���λ���ǣ�������
A.2.15B.2.16C.2.17D.2.20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=7��AC=5��BC=6����ABC����ACB��ƽ�����ཻ�ڵ�D������D��BC��ƽ���߽�AB�ڵ�E����AC�ڵ�F������AEF���ܳ�Ϊ�� ��

A.9 B.11 C.12 D.13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB������������A��B����֮��ľ���AB=|a��b|��
����ʽ��|x��2|�ļ��������������ϱ�ʾx�ĵ����ʾ2�ĵ�֮��ľ��룮����������ش��������⣺
�������ϱ�ʾ2��5����֮��ľ����� �� �����ϱ�ʾ1�ͩ�3������֮��ľ����� ��
�������ϱ�ʾx�ͩ�2������֮��ľ����ʾΪ ��
�������ϱ�ʾx�ĵ㵽��ʾ1�ĵ�ľ�����������ʾ��3�ĵ�ľ���֮�Ϳɱ�ʾΪ��|x��1|+|x+3|����|x��1|+|x+3|����Сֵ�� ��
����|x��3|+|x+1|=8����x=![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|a|=��a����aΪ��������
A. a�Ǹ��� B. a������ C. a=0 D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
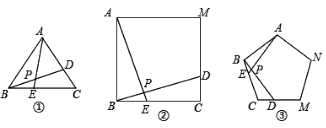
����Ŀ����ͼ�����������У���E��D�ֱ�������ABC�����ı���ABCM���������ABCMN����C��Ϊ��������������ϵĵ㣬��BE=CD��DB��AE��P�㣮
��1����ͼ���У���APD�Ķ���Ϊ_______����2��ͼ���У���APD�Ķ���Ϊ_________��
��3��ͼ���У���APD�Ķ���Ϊ_______��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com