
 如图,点G、D、C在直线a上,点E、F、A、B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合时停止运动.在运动过程中,△GEF与矩形ABCD(AB>EF)重合部分的面积S随时间t变化的图象大致是( )
如图,点G、D、C在直线a上,点E、F、A、B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合时停止运动.在运动过程中,△GEF与矩形ABCD(AB>EF)重合部分的面积S随时间t变化的图象大致是( )| A. | 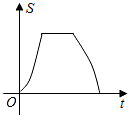 | B. | 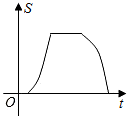 | C. |  | D. | 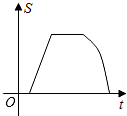 |
分析 理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.
解答 解:根据题意可得:
①F、A重合之前没有重叠面积,
②F、A重叠之后到E与A重叠前,设AE=a,EF被重叠部分的长度为(t-a),则重叠部分面积为S=$\frac{1}{2}$(t-a)•(t-a)tan∠EFG=$\frac{1}{2}$(t-a)2tan∠EFG,
∴是二次函数图象;
③△EFG完全进入且F与B重合之前,重叠部分的面积是三角形的面积,不变,
④F与B重合之后,重叠部分的面积等于S=S△EFG-$\frac{1}{2}$(t-a)2tan∠EFG,符合二次函数图象,直至最后重叠部分的面积为0.
综上所述,只有B选项图形符合.
故选:B.
点评 本题考查动点问题的函数图象,学会分段讨论是解题的关键,需要构建函数解决问题,属于中考常考题型.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:选择题
| A. | -9在实数范围内没有平方根 | B. | $\sqrt{324}=±18$ | ||
| C. | ±6是216的立方根 | D. | 平方根等于其本身的数有0,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+1 | B. | 10x+1 | C. | 100x+1 | D. | 1000x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1>x2 | B. | x1=x2 | C. | x1<x2 | D. | 不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
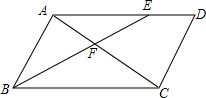 如图,在?ABCD中,点E在AD边上,BE交对角线AC于点F,则下列各式错误的是( )
如图,在?ABCD中,点E在AD边上,BE交对角线AC于点F,则下列各式错误的是( )| A. | $\frac{AF}{CF}=\frac{EF}{BF}$ | B. | $\frac{AF}{BF}=\frac{EF}{CF}$ | C. | $\frac{BF}{BE}=\frac{CF}{AC}$ | D. | $\frac{AF}{EF}=\frac{CF}{BF}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com