
 �۲�����ÿ�����������ϵĶ�Ӧ��֮��ľ��룺4��-2��3��5��-2��-6��-4��3�����ش����и��⣺
�۲�����ÿ�����������ϵĶ�Ӧ��֮��ľ��룺4��-2��3��5��-2��-6��-4��3�����ش����и��⣺���� ��1���������ᷢ�֣�����ľ���Ϊ��ʾ��������IJ�ľ���ֵ��
��2�����ݷ��ֵĹ��ɴ��뼴�ɣ�
��3���������ó���|x-2|+|x+6|����Сֵ����ʾ��x��2��-6����ľ���֮����С����Ϊ8��
��� �⣺��1��4��-2�ľ��룺6=|-2-4|��
3��5�ľ��룺2=|5-3|��
-2��-6�ľ��룺4=|-2-��-6��|��
-4��3�ľ��룺7=|3-��-4��|��
��AB=|a-b|��
�ʴ�Ϊ��|a-b|��
��2��AB=|x-��-1��|=|x+1|��
�ʴ�Ϊ��|x+1|��
��3��|x-2|+|x+6|��ʾ��x��2��-6����ľ���֮�ͣ�
�������Сֵ����xһ����2��-6֮�䣬����СֵΪ8��
�ʴ�Ϊ��8��
���� ���⿼��������������ľ��룬����������ľ��������ֵ�йأ���ʾ����������ľ���ֵ���������������ν�ϵ�˼�룬�ó����ɣ���������㣮


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
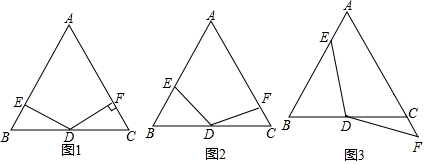
 ��ͼ������ֽƬABCD�У���A=60�㣬��ֽƬ�۵�����A��D�ֱ�����A�䣬D�䴦����A��D�侭����B��EFΪ�ۺۣ���D��F��CDʱ��$\frac{CF}{BE}$��ֵΪ��������
��ͼ������ֽƬABCD�У���A=60�㣬��ֽƬ�۵�����A��D�ֱ�����A�䣬D�䴦����A��D�侭����B��EFΪ�ۺۣ���D��F��CDʱ��$\frac{CF}{BE}$��ֵΪ��������| A�� | $\frac{3-\sqrt{3}}{2}$ | B�� | $\frac{3+\sqrt{3}}{2}$ | C�� | $\frac{3-\sqrt{3}}{3}$ | D�� | $\frac{3+\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ABCD��ԲO���ڽ��ı��Σ�BC��ԲO��ֱ������ACB=20�㣬DΪ��$\widehat{AC}$���е㣬���DAC�Ķ�����
��ͼ��ABCD��ԲO���ڽ��ı��Σ�BC��ԲO��ֱ������ACB=20�㣬DΪ��$\widehat{AC}$���е㣬���DAC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
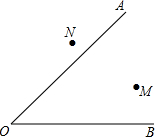 ��֪��AOB����M��N���ڡ�AOB���ڲ�����һ��P��ʹ��P����AOB�����߾�����ȣ���PM=PN��Ҫ�߹���ͼ��������ͼ�ۼ�����д��������
��֪��AOB����M��N���ڡ�AOB���ڲ�����һ��P��ʹ��P����AOB�����߾�����ȣ���PM=PN��Ҫ�߹���ͼ��������ͼ�ۼ�����д���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪�����ߵIJ���ʽΪy=-x2+6x+c��
��֪�����ߵIJ���ʽΪy=-x2+6x+c���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
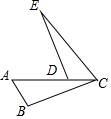 ��֪����ͼ����A��D��C��ͬһֱ���ϣ�AB��EC��AC=CE����B=��EDC��
��֪����ͼ����A��D��C��ͬһֱ���ϣ�AB��EC��AC=CE����B=��EDC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x+2y=6xy | B�� | 2a2+3a3=5a3 | C�� | 3mn-3nm=0 | D�� | 7x-5x=2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com