
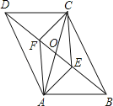
【题目】如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.

【答案】(1)作图见解析;(2)证明见解析.
【解析】(1)由角平分线的作法容易得出结果,在AD上截取AF=AB,连接EF;画出图形即可;(2)由平行四边形的性质和角平分线得出∠BAE=∠AEB,证出BE=AB,由(1)得:AF=AB,得出BE=AF,即可得出结论.
解:(1)如图AE就是所要求的角平分线。
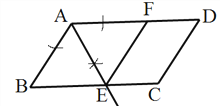
(2)四边形ABEF是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,∴BE=AB,
由(1)得:AF=AB,
∴BE=AF,又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴四边形ABEF是菱形.


科目:初中数学 来源: 题型:
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
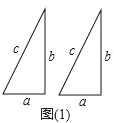
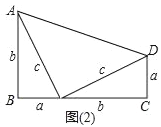
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
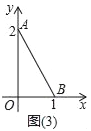
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…,Cn在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标:_____,写出一个满足条件的在y轴上的点坐标:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,2016排列成如图所示的形式.

(1)用一个矩形随意框住4个数,把其中最小的数记为![]() ,另三个数用含
,另三个数用含![]() 式子表示出来,当被框住的4个数之和等于418时,
式子表示出来,当被框住的4个数之和等于418时,![]() 值是多少?
值是多少?
(2)被框住的4个数之和能否等于724?如果能,请求出此时x值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两同学用两枚质地均匀的骰子作游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局. 根据上述规则,解答下列问题;
(1)随机掷两枚骰子一次,用列表法求点数和为8的概率;
(2)甲先随机掷两枚骰子一次,点数和是7,求乙随机掷两枚骰子一次获胜的概率. (骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元;
(2)若体育老师带了8000元去购买这种篮球与足球共100个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某停车场收费标准分为中型汽车和小型汽车两种,某两天这个停车场的收费情况如下表:
中型汽车数量 | 小型汽车数量 | 收取费用 | |
第一天 | 15辆 | 35辆 | 360元 |
第二天 | 18辆 | 20辆 | 300元 |
(1)中型汽车和小型汽车的停车费每辆多少元?
(2)某天停车场共停车70辆,若收取的停车费用高于500元,则中型汽车至少有多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OD恰为∠BOE的平分线.
(1)图中∠BOC的补角是 把符合条件的角都填出来);
(2)若∠AOD=145°,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com