
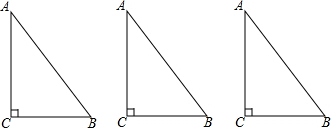
分析 根据题目要求扩充成AC为直角边的等腰直角三角形,即AC=BC,∠C=90°,然后由勾股定理求得AB的长,最后求出扩充后的等腰直角三角形的周长即可.
解答 解:如图1,延长BC到D,使AB=AD,连接AD,则AB=AD=10时,可求CD=CB=6得△ABD的周长为32m;
②如图2,当AB=BD=10时,可求CD=4,
由勾股定理得:AD=4$\sqrt{5}$得△ABD的周长为(20+4$\sqrt{5}$)m.
③如图3,当AB为底时,设AD=BD=x,则CD=x-6,由勾股定理得:x=$\frac{25}{3}$得△ABD的周长为$\frac{80}{3}$m. 
点评 本题主要考查对勾股定理,等腰三角形的性质等知识点的理解和掌握,能通过分类求出等腰三角形的所有情况是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 11.4×102 | B. | 1.14×103 | C. | 1.14×104 | D. | 1.14×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
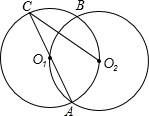 如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1,并延长交⊙O1于点C,则∠ACO2的度数为( )
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1,并延长交⊙O1于点C,则∠ACO2的度数为( )| A. | 60° | B. | 45° | C. | 30° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=$\frac{\sqrt{3}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO′B,则点O′的坐标是( )
如图,直线y=$\frac{\sqrt{3}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO′B,则点O′的坐标是( )| A. | (-$\sqrt{3}$,3) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
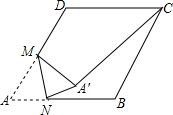 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )
如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )| A. | $\sqrt{7}$ | B. | $\sqrt{7}-1$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.
如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向C处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.1h,轮船甲行驶至B处,轮船乙行驶至D处,测得∠DBO=58°,此时B处距离码头O多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com