
| A. | 2017 | B. | 1 | C. | 2016 | D. | 2 |
分析 首先定义的新运算方法,可得a2=a1+1-5([$\frac{2-1}{5}$]-[$\frac{2-2}{5}$])=1+1=2,a3=a2+1-5([$\frac{3-1}{5}$]-[$\frac{3-2}{5}$])=2+1=3,同理,可得a4=4,a5=5,a6=1,a7=2,…,所以这列数是1、2、3、4、5、1、2、3、4、5、…,每5个数是一个循环;然后用2016除以4,根据余数的情况判断出a2016的值为多少即可.
解答 解:∵a1=1,
∴a2=a1+1-5([$\frac{2-1}{5}$]-[$\frac{2-2}{5}$])=1+1=2,
a3=a2+1-5([$\frac{3-1}{5}$]-[$\frac{3-2}{5}$])=2+1=3,
同理,可得a4=4,a5=5,a6=1,a7=2,…,
∴这列数是1、2、3、4、5、1、2、3、4、5、…,每5个数是一个循环;
∵2016÷5=403…1,
∴a2016=1.
故选B.
点评 此题主要考查了数字的变化类,探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:这列数是1、2、3、4、5、1、2、3、4、5、…,每5个数是一个循环.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:填空题
 如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,DO:BO=1:2,点E在CB的延长线上,如果S△AOD:S△ABE=1:3,那么BC:BE=2:1.
如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,DO:BO=1:2,点E在CB的延长线上,如果S△AOD:S△ABE=1:3,那么BC:BE=2:1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
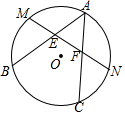 如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形.
如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
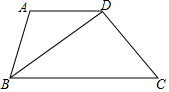 如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,则tan∠DBC=$\frac{3}{4}$.
如图,在梯形ABCD中,AD∥BC,BD平分∠ABC,且CD⊥BD,若AD=5,BD=CD+2,则tan∠DBC=$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com