
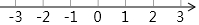
分析 (1)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
(2)利用分式的混合运算,化简原式,再把当x=tan60°+(-$\frac{1}{2}$)-2+50-$\sqrt{3}$,代入化简后的式子,计算即可.
解答 解:(1)$\left\{\begin{array}{l}{4x>2x-6①}\\{\frac{x-1}{3}≤\frac{x+1}{9}②}\end{array}\right.$,
∵解不等式①得:x>-3,
解不等式②得:x≤2,
∴不等式组的解集为-3<x≤2,
在数轴上表示不等式组的解集为: ;
;
(2)(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$=$\frac{x-2}{x-1}$•$\frac{(x+1)(x-1)}{(x-2)^{2}}$=$\frac{x+1}{x-2}$,
当x=tan60°+(-$\frac{1}{2}$)-2+50-$\sqrt{3}$=5时,
原式=2.
点评 本题考查了分式的化简求值、特殊三角函数值的知识,解决此类题目的关键是熟记特殊角的三角函数值.


科目:初中数学 来源: 题型:解答题
| 日期x | 1 | 2 | 3 | 4 |
| 水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 向上攀登的高度x/km | 0.5 | 1.0 | 1.5 | 2.0 |
| 气温y/℃ | 2.0 | -0.9 | -4.1 | -7.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
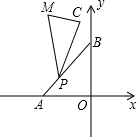 如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度.
如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com