
【题目】如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.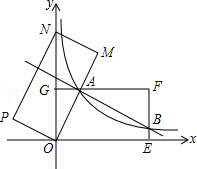
(1)求图象经过点A的反比例函数的解析式;
(2)设(2)中的反比例函数图象交EF于点B,直接写出直线AB的解析式.
【答案】
(1)
解:∵∠OGA=∠M=90°∠GOA=∠MON
∴△OGA∽△OMN,
∴ ![]()
∴ ![]() ,
,
解得AG=1.
设反比例函数y= ![]() ,把A(1,2)代入得k=2,
,把A(1,2)代入得k=2,
∴过点A的反比例函数的解析式为:y= ![]() .
.
(2)
解:∵点B的横坐标为4,x=4代y= ![]() 中y=
中y= ![]() ,故(4,
,故(4, ![]() )
)
设直线AB的解析式y=mx+n,把A(1,2)、B(4, ![]() )代入,得
)代入,得
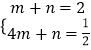 ,
,
解得 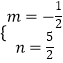 .
.
∴直线AB的解析式y=﹣ ![]() x+
x+ ![]() .
.
【解析】(1)先根据两个角对应相等,即可证明△OGA和△OMN相似,要求反比例函数的解析式,则需求得点A的坐标,即要求得AG的长,根据旋转的两个图形全等的性质以及相似三角形的对应边的比相等可以求解;(2)要求直线AB的解析式,主要应求得点B的坐标.根据点B的横坐标是4和(1)中求得的反比例函数的解析式即可求得.再根据待定系数法进行求解.
【考点精析】本题主要考查了反比例函数的性质的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1) 求出△ABC的面积
(2) 在图形中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1、B1、C1的坐标
(3) 是否存在一点P到AC、AB的距离相等,同时到点A、点B的距离也相等.若存在保留作图痕迹标出点P的位置,并简要说明理由;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4 m的半圆,其边缘AB=CD=20 m,点E在CD上,CE=4 m,一滑行爱好者从A点滑到E点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)

查看答案和解析>>
科目:初中数学 来源: 题型:
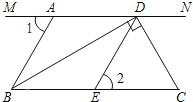
【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 与 DE 平行吗?请说明理由;
(2)若 DC 是∠NDE 的平分线.
①试说明∠ABC=∠C;
②试说明 BD 是∠ABC 的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
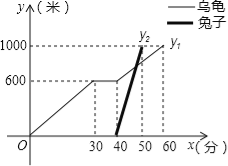
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),C(0,4)两点,与x轴交于另一点B,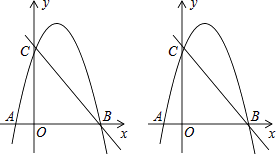
(1)求抛物线的解析式;
(2)求P在第一象限的抛物线上,P点的横坐标为t,过点P向x轴做垂线交直线BC于点Q,设线段PQ的长为m,求m与t之间的函数关系式并求出m的最大值;
(3)在(2)的条件下,抛物线上一点D的纵坐标为m的最大值,连接BD,在抛物线是否存在点E(不与点A,B,C重合)使得∠DBE=45°?若不存在.请说明理由;若存在请求E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一间阶梯教室,第1排的座位数为a,从第2排开始,每一排都比前一排增加b个座位,
(1)请你在下表的空格里填写一个适当的式子:
第1排座位数 | 第2排座位数 | 第3排座位数 | 第4排座位数 | …… |
a | a+b | a+2b` | …… |
(2)已知第4排有18个座位,第15排的座位数是第5排座位数的2倍,求第21排有多少个座位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳上网费的方式有:方式一:每月80元包月;方式二:每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示;方式三:以0小时为起点,每小时收费1.6元,月收费不超过120元.若设一用户每月上网x小时,月上网费为y元.

(1)根据图象,写出方式二中y(元)与x(小时)的函数关系式;
(2)试写出方式三中y(元)与x(小时)的函数关系式;
(3)若此用户每月上网60小时,选用哪种方式上网其费用最少?最少费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com