
【题目】如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
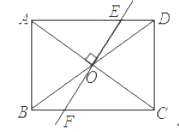
A.1B.![]() C.2D.
C.2D.![]()
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某宾馆大厅要铺圆环形的地毯,工人师傅只测量了与小圆相切的大圆的弦AB的长,就计算出了圆环的面积,若测量得AB的长为20米,则圆环的面积为( )
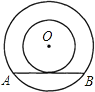
A. 10平方米B. 10π平方米C. 100平方米D. 100π平方米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:直线l及直线l上一点P.
![]()
求作:直线PQ,使得PQ⊥l.
作法:如图,
![]()
①在直线l上取一点A(不与点P重合),分别以点P,A为圆心,AP长为半径画弧,两弧在直线l的上方相交于点B;
②作射线AB,以点B为圆心,AP长为半径画弧,交AB的延长线于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接BP,
∵ = = =AP,
∴点A,P,Q在以点B为圆心,AP长为半径的圆上.
∴∠APQ=90°( ).(填写推理的依据)
即PQ⊥l.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队5名场上队员的身高(单位:cm)是:183、187、190、200、210,现用一名身高为195cm的队员换下场上身高为210 cm的队员,与换人前相比,场上队员的身高 ( )
A.平均数变大,方差变大B.平均数变小,方差变小
C.平均数变大,方差变小D.平均数变小,方差变大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
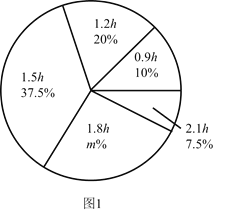
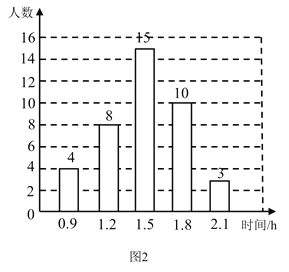
(Ⅰ)本次接受调查的初中学生人数为 ,图1中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有1200名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(﹣1,0).下列结论:①a+c=1;②b2﹣4ac≥0;③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为x=﹣![]() .其中结论正确的个数有( )
.其中结论正确的个数有( )
A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题:两个重叠的正多边形,其中的一个绕某一顶点旋转所形成的有关问题.
实验与论证:
设旋转角∠A1A0B1=α(α<∠A1A0A2),θ3、θ4、θ5、θ6所表示的角如图所示.
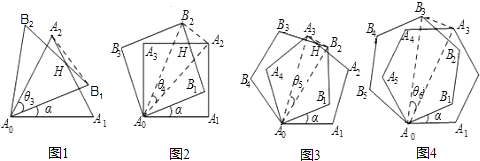
(1)用含α的式子表示角的度数:θ3= ,θ4= ,θ5= ;
(2)图1﹣图4中,连接A0H时,在不添加其他辅助线的情况下,是否存在与直线A0H垂直且被它平分的线段?若存在,请选择其中的一个图给出证明;若不存在,请说明理由;
归纳与猜想:
设正n边形A0A1A2…An﹣1与正n边形A0B1B2…Bn﹣1重合(其中,A1与B1重合),现将正多边形A0B1B2…Bn﹣1绕顶点A0逆时针旋转α(0°<α<![]() °);
°);
(3)设θn与上述“θ3、θ4、…”的意义一样,请直接写出θn的度数;
(4)试猜想在正n边形的情形下,是否存在与直线A0H垂直且被它平分的线段?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
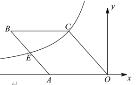
【题目】如图,在平面直角坐标系中,菱形 ABCO 的一边 OA 在 x 轴上,![]() ,反比例函数
,反比例函数![]() 过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com