
分析 分式方程变形后,设$\frac{{x}^{2}-5}{x-1}$=y,求出解得到y的值,即可确定出x的值.
解答 解:设$\frac{{x}^{2}-5}{x-1}$=y,方程变形得:y+$\frac{10}{y}$=7,
去分母得:y2-7y+10=0,即(y-2)(y-5)=0,
解得:y=2或y=5,
∴$\frac{{x}^{2}-5}{x-1}$=2或$\frac{{x}^{2}-5}{x-1}$=5,
整理得:x2-2x-3=0或x2-5x=0,
解得:x=3或x=-1或x=0或x=5,
经检验x=3,x=-1,x=0,x=5都为分式方程的解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
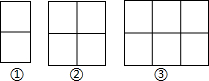
| 图形编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 图形中的棋子 | 6 | 9 | 12 | 15 | 18 | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.
如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB=10cm,点C为射线AB上的点,且BC=6cm,点M为线段AC的中点、点N为线段BC的中点.
如图,已知线段AB=10cm,点C为射线AB上的点,且BC=6cm,点M为线段AC的中点、点N为线段BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,AB=CD,AD=CB,沿对角线AC把四边形ABCD剪开,得到两个三边互不相等的锐角三角形.如果让△ABC不动,变换△ADC的位置,使它与△ABC的一边重合,重新拼合成新的四边形,那么这样不同的“拼合四边形”一共有( )
如图,在四边形ABCD中,AB=CD,AD=CB,沿对角线AC把四边形ABCD剪开,得到两个三边互不相等的锐角三角形.如果让△ABC不动,变换△ADC的位置,使它与△ABC的一边重合,重新拼合成新的四边形,那么这样不同的“拼合四边形”一共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中D、E、F分别是各边的中点,连接AE、DF.
如图,△ABC中D、E、F分别是各边的中点,连接AE、DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com