
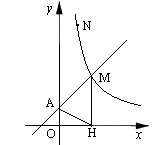
如图,直线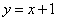 与y轴交于A点,与反比例函数
与y轴交于A点,与反比例函数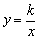 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO= .
.
(1)求k的值;
|
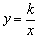 (x>0)图像上的点,
(x>0)图像上的点, 在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
由y=x+1可得A(0,1),即OA=1
∵tan∠AHO=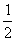 ,∴OH=2
,∴OH=2
∵MH⊥x轴,∴点M的横坐标为2.
∵点M在直线y=x+1上,
∴点M的纵坐标为3.即M(2,3)
∵点M在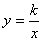 上,∴k=2×3=6.
上,∴k=2×3=6.
(2)∵点N(1,a)在反比例函数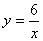 的图像上,
的图像上,
∴a=6.即点N的坐标为(1,6) 过N作N关于y轴的对称点N1,连接MN1,交y轴于P(如图)
此时PM+PN最小.
∵N与N1关于y轴的对称,N点坐标为(1,6),
∴N1的坐标为(-1,6)
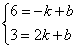 设直线MN1的解析式为y=kx+b.
设直线MN1的解析式为y=kx+b.
把M,N1 的坐标得
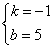
解得
∴直线MN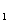 的解析式为
的解析式为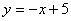 .
.
令x=0,得y=5.
∴P点坐标为(0,5)


科目:初中数学 来源: 题型:
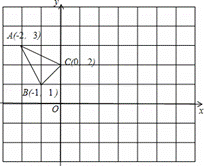
△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有2个,黑球有1个,绿球有3个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
A.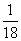 B.
B.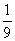 C.
C.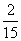 D.
D. 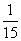
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,两圆的圆心坐标分别为(-3,0)和(0,4),半径是方程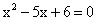 的两根,那么这两圆的位置关系是( )(原创)
的两根,那么这两圆的位置关系是( )(原创)
A、外离 B、相切 C、相交 D、内含
查看答案和解析>>
科目:初中数学 来源: 题型:
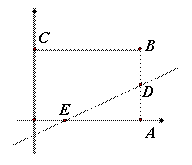
如图,矩形OABC顶点A(6,0)、C(0,4),直线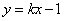 分别交BA、OA于点D、E,且D为BA中点。
分别交BA、OA于点D、E,且D为BA中点。
(1)求k的值及此时△EAD的面积;
(2)现向矩形内随机投飞镖,求飞镖落在△EAD内的概率。(若投在边框上则重投)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com