
【题目】如图所示,OM平分∠BOC,ON平分∠AOC, 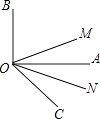
(1)若∠AOB=90°,∠AOC=30°,求∠MON的度数;
(2)若(1)中改成∠AOB=60°,其他条件不变,求∠MON的度数;
(3)若(1)中改成∠AOC=60°,其他条件不变,求∠MON的度数;
(4)从上面结果中看出有什么规律?
【答案】
(1)解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=120°,
∴∠MOC=60°,
∵∠AOC=30°,
∴∠CON=15°,
∴∠MON=∠MOC﹣∠NOC=60°﹣15°=45°
(2)解:∵∠AOB=60°,∠AOC=30°,
∴∠BOC=90°,
∴∠MOC=45°,
∵∠AOC=30°,
∴∠CON=15°,
∴∠MON=∠MOC﹣∠NOC=45°﹣15°=30°
(3)解:∵∠AOB=90°,∠AOC=60°,
∴∠BOC=150°,
∴∠MOC=75°,
∵∠AOC=60°,
∴∠CON=30°,
∴∠MON=∠MOC﹣∠NOC=75°﹣30°=45°
(4)解:从上面结果中看出∠MON的大小是∠AOB的一半,与∠AOC无关
【解析】(1)由∠AOB=90°,∠AOC=30°,易得∠BOC,可得∠MOC,由角平分线的定义可得∠CON,可得结果;(2)同理(1)可得结果;(3)同理(1)可得结果;(4)根据结果与∠AOB,∠AOC的度数归纳规律.
【考点精析】根据题目的已知条件,利用角的平分线的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.

(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空
依据下列解方程 ![]() 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:去分母,得3(3x+5)=2(2x﹣1).()
去括号,得9x+15=4x﹣2()
(),得9x﹣4x=﹣15﹣2.()
合并,得5x=﹣17()
(),得 ![]() .()
.()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )
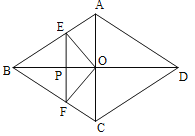
A. 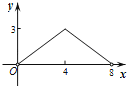 B.
B. 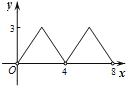
C. 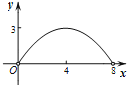 D.
D. 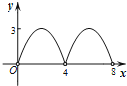
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费,如表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
17吨及以下 | a | 0.80 |
超过17吨不超过30吨的部分 | b | 0.80 |
超过30吨的部分 | 6.0 | 0.80 |
(说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
(1)已知小王家2016年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元,求a、b的值.
(2)如果6月份小王家计划水费不超过140元,那么他家本月用水量最多为多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com