
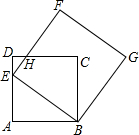
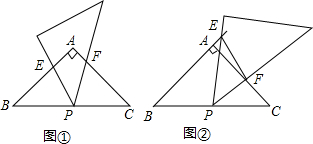
 如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.
如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.分析 (1)根据正方形的性质得到∠D=∠A=∠BEF=90°,根据余角的性质得到∠AEB=∠DHE,根据相似三角形的想知道的$\frac{DH}{AE}=\frac{DE}{AB}$,代入数据即可得到结论;
(2)过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,根据已知条件得到AE=12,求得DE=4,根据余角的性质得到∠MEF=∠ABE,等量代换得到tan∠MEF=$\frac{3}{4}$求得ME=16,FM=12,根据勾股定理即可得到结论;
(3)由于S△CEF=S△CHF+S△CHE=$\frac{1}{2}$CH•EM,根据全等三角形的性质得到EM=AB=16,求得S△CEF=8CH,根据相似三角形的性质得到$\frac{DE}{AB}=\frac{DH}{AE}$,设AE为x,于是得到DH=$\frac{1}{16}$(-x2+16x)=-$\frac{1}{16}$(x-8)2+4≤4,即可得到结论.
解答 解:(1)∵四边形ABCD和四边形BGFE是正方形,
∴∠D=∠A=∠BEF=90°,
∴∠AEB+∠DEH=∠DEH+∠DHE=90°,
∴∠AEB=∠DHE,
∴△EDH∽△BAE,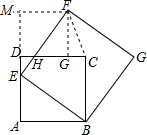
∴$\frac{DH}{AE}=\frac{DE}{AB}$,
∵E为边AD的中点,
∴DE=AE=8,
∴$\frac{DH}{8}=\frac{8}{16}$,
∴DH=4;
(2)过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,
∵tan∠ABE=$\frac{3}{4}$,AB=16,
∴AE=12,
∴DE=4,
∵∠MEF+∠AEB=∠AEB+∠ABE=90°,
∴∠MEF=∠ABE,
∴tan∠MEF=$\frac{3}{4}$,
∴ME=16,FM=12,
∴DM=12,
∴DM=MF,
∴四边形DGFM是正方形,
∴FG=12,HG=9,
∴CG=4,
∴FC=$\sqrt{F{G}^{2}+C{G}^{2}}$=4$\sqrt{10}$;
(3)∵S△CEF=S△CHF+S△CHE=$\frac{1}{2}$CH•EM,
∵△EMF≌△BAE,
∴EM=AB=16,
∴S△CEF=8CH,
∵△EDH∽△BAE,
∴$\frac{DE}{AB}=\frac{DH}{AE}$,
设AE为x,则DH=$\frac{1}{16}$(-x2+16x)=-$\frac{1}{16}$(x-8)2+4≤4,
∴DH≤4,
∴CH≥12,CH最小值是12,
∴△CEF面积的最小值是96.
点评 本题考查了正方形的性质、全等三角形的判定及性质、相似三角形的判定及性质、三角形的面积公式及二次函数的性质,解题的关键是找出线段DN的最大值.本题属于中档题,难度不大,解决该题型题目时,根据三角形的面积公式找出其去最值的条件,再结合二次函数的性质去解决最值问题.


科目:初中数学 来源: 题型:选择题
 已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点F的运动时间为y秒,当y的值为( )秒时,△ABF和△DCE全等.
已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点F的运动时间为y秒,当y的值为( )秒时,△ABF和△DCE全等.| A. | 1 | B. | 1或3 | C. | 1或7 | D. | 3或7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
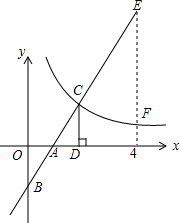 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com