
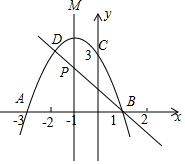
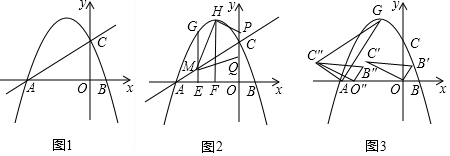
 如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴相交于A(-3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.分析 (1)根据C、D关于对称轴x=-1对称,C(0,3),可以求出点D坐标.
(2)设二次函数解析式为y=a(x+3)(x-1),把C(0,3)代入得到求出a即可.
(3)一次函数值小于二次函数值,在图象上一次函数的图象在二次函数的图象下面即可写出x的范围.
(4)设M(m,-m2-2m+3),作MP∥y轴,交BD于P,根据S△MBD=S△PMD+S△PMB构建二次函数,利用二次函数的性质即可解决问题.
解答 解:(1)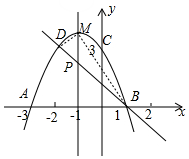 由题意可知C、D关于对称轴x=-1对称,C(0,3),
由题意可知C、D关于对称轴x=-1对称,C(0,3),
∴D(-2,3)
故答案为-2,3.
(2)设二次函数解析式为y=a(x+3)(x-1),
把C(0,3)代入得到,a=-1,
∴二次函数解析式为y=-(x+3)(x-1),
即y=-x2-2x+3.
(3)由图象可知,一次函数值小于二次函数值的x的取值范围-2<x<1.
(4)设M(m,-m2-2m+3),作MP∥y轴,交BD于P,
∵D(-2,3),B(1,0),
∴直线BD的解析式为y=-x+1,
∴p(m,-m+1),
∴S△MBD=S△PMD+S△PMB=$\frac{1}{2}$•(-m2-2m+3+m-1)•3=-$\frac{3}{2}$(m+$\frac{1}{2}$)2+$\frac{27}{8}$.
∵-$\frac{3}{2}$<0,
∴m=-$\frac{1}{2}$时,△MBD的面积最大值为$\frac{27}{8}$.
点评 本题考查二次函数综合题、一次函数、三角形的面积、最值问题等知识,解题的关键是学会构建二次函数解决最值问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | (x-1)(x+2)=x2+3 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}-2$=0 | C. | (x-1)2=2x-2 | D. | ax2+2x-1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
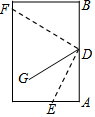 小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
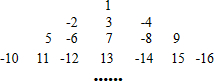
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为(45,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com