
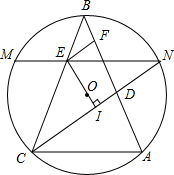
 长线交⊙O于N,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,NE的延长线交⊙O于M.
长线交⊙O于N,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,NE的延长线交⊙O于M. |
| MB |
 |
| BN |
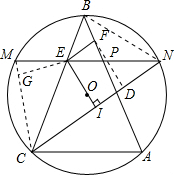 证明:(1)如图,设直线OE与CM交于点I,
证明:(1)如图,设直线OE与CM交于点I,
|
 |
| BC |
 |
| AB |
 |
| MC |
 |
| NA |
 |
| MB |
 |
| BN |
|
|


科目:初中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| b |
 (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
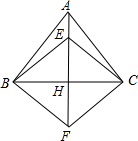 如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,查看答案和解析>>
科目:初中数学 来源: 题型:
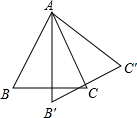 如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转
如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com