
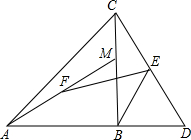
 如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )
如图,在等腰直角△ABC中,AB=BC,点M是BC边上任意一点,点D是AB的延长线上一点,且BM=BD;又有点E、F分别是CD、AM边的中点,连结FE、EB.下列结论一定正确的有( )| A. | ①② | B. | ①②③ | C. | ①②③④ | D. | ①②④ |
分析 ①求出∠ABM=∠CBD,根据SAS推出全等即可;
②根据全等求出AM=DC,推出BE=BF,求出∠EBF=90°,即可得出∠BEF=45°;
④设EF=3a,AC=5a,由勾股定理求出AB=BC=$\frac{5\sqrt{2}}{2}$a,BF=BE=$\frac{3\sqrt{2}}{2}$a,求出AM=2BF=3$\sqrt{2}$a,解直角三角形求出即可;
③△AMB≌△CDB,得到BM=BD=$\sqrt{11}$a,得到$\frac{BD}{AB}$=$\frac{\sqrt{11}a}{\frac{5\sqrt{2}}{2}a}$=$\frac{\sqrt{22}}{5}$≠$\frac{3}{5}$=$\frac{EF}{AC}$,故③错误
解答 解:①∵∠ABC=90°,
∴∠ABM=∠CBD=90°,
∵在△AMB和△CDB中
$\left\{\begin{array}{l}{AB=BC}\\{∠ABM=∠CBD}\\{BM=BD}\end{array}\right.$,
∴△AMB≌△CDB(SAS),故①正确;
②∠BEF的度数不发生变化,
理由是:连接BF,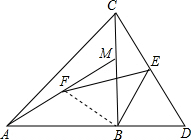
∵△AMB≌△CDB,
∴∠DCB=∠MAB,AM=DC,
∵E、F分别为DC、AM中点,∠ABM=∠CBD=90°,
∴BE=DE=CE$\frac{1}{2}$CD,BF=MF=AF=$\frac{1}{2}$AM,
∴BE=BF,∠BAF=∠FBA,∠EBD=∠D,
∵∠D+∠DCB=90°,
∴∠FBA+∠EBD=90,
∴∠FBE=180°-90°=90°,
∵BE=BF,
∴∠BEF=45°,故②正确;
④设EF=3a,AC=5a,
∵∠ABC=90°,AB=BC,
∴由勾股定理得:AB=BC=$\frac{5\sqrt{2}}{2}$a,
同理:BF=BE=$\frac{3\sqrt{2}}{2}$a,
∴AM=2BF=3$\sqrt{2}$a,
∴$\frac{AB}{AM}$=$\frac{5}{6}$,故④正确;
③∵△AMB≌△CDB,
∴BM=BD=$\sqrt{11}$a,
∴$\frac{BD}{AB}$=$\frac{\sqrt{11}a}{\frac{5\sqrt{2}}{2}a}$=$\frac{\sqrt{22}}{5}$≠$\frac{3}{5}$=$\frac{EF}{AC}$,故③错误.
故选D.
点评 本题考查了等腰直角三角形性质和判定,直角三角形斜边上中线,全等三角形的性质和判定,解直角三角形,勾股定理的应用,关键是推出△AMB≌△CDB和求出△EBF是等腰直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标.
如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,若点P的坐标为(-2,t),当PA=AB时,求点A的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a是无理数 | B. | a是方程x2-8=0的解 | ||
| C. | a是8的算术平方根 | D. | a满足不等式$\frac{2x-4}{3}>1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?
如图所示,折线ABC是在某市乘出租车需付车费y(元)与行车里程x(千米)之间的函数关系图象.若某人付费30.8元,出租车行驶了多少千米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
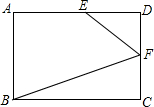 已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.
已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.
如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
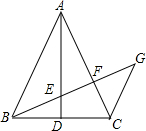 如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.
如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
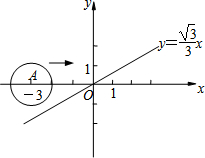 如图,在平面直角坐标系中,x轴上一点A从点(-3,0)出发沿x轴向右平移,当以A为圆心,半径为1的圆与函数y=$\frac{\sqrt{3}}{3}$x的图象相切时,点A的坐标变为( )
如图,在平面直角坐标系中,x轴上一点A从点(-3,0)出发沿x轴向右平移,当以A为圆心,半径为1的圆与函数y=$\frac{\sqrt{3}}{3}$x的图象相切时,点A的坐标变为( )| A. | (-2,0) | B. | (-$\sqrt{3}$,0)或($\sqrt{3}$,0) | C. | (-$\sqrt{3}$,0) | D. | (-2,0)或(2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com