
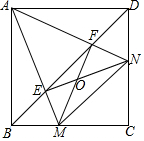
 如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.
如图,已知正方形ABCD,M,N分别是BC,CD上的点,∠MAN=45°,连接BD分别交AM,AN于E,F,下面结论错误的是⑤.分析 将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.证明△MAN≌△HAN,得到MN=NH,根据三角形周长公式计算判断①;
根据全等三角形的性质判断②;
将△ADF绕点A顺时针性质90°得到△ABH,连接HE.证明△EAH≌△EAF,得到∠HBE=90°,根据勾股定理计算判断③;
根据等腰直角三角形的判定定理判断④;
根据等腰直角三角形的性质、三角形的面积公式计算,判断⑤,
根据点A到MN的距离等于正方形ABCD的边长、三角形的面积公式计算,判断⑥.
解答 解:将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.
则∠DAH=∠BAM,
∵四边形ABCD是正方形,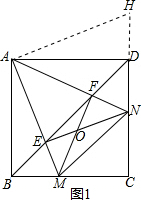
∴∠BAD=90°,
∵∠MAN=45°,
∴∠BAN+∠DAN=45°,
∴∠NAH=45°,
在△MAN和△HAN中,
$\left\{\begin{array}{l}{AM=AH}\\{∠MAN=∠HAN}\\{AN=AN}\end{array}\right.$,
∴△MAN≌△HAN,
∴MN=NH=BM+DN,
∴△CMN的周长=CM+CN+MN=CM+BM+CN+DN=CB+CD,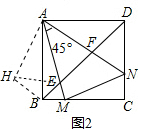
∴△CMN的周长等于正方形ABCD的边长的两倍,①结论正确;
∵△MAN≌△HAN,
∴点A到MN的距离等于正方形ABCD的边长AD,②结论正确;
如图2,将△ADF绕点A顺时针性质90°得到△ABH,连接HE.
∵∠DAF+∠BAE=90°-∠EAF=45°,∠DAF=∠BAE,
∴∠EAH=∠EAF=45°,
∵EA=EA,AH=AD,
∴△EAH≌△EAF,
∴EF=HE,
∵∠ABH=∠ADF=45°=∠ABD,
∴∠HBE=90°,
在Rt△BHE中,HE2=BH2+BE2,
∵BH=DF,EF=HE,
∵EF2=BE2+DF2,③结论正确;
∵四边形ABCD是正方形,
∴∠ADC=90°,∠BDC=∠ADB=45°,
∵∠MAN=45°,
∴∠EAN=∠EDN,
∴A、E、N、D四点共圆,
∴∠ADN+∠AEN=180°,
∴∠AEN=90°
∴△AEN是等腰直角三角形,
同理△AFM是等腰直角三角形;④结论正确;
∵△AEN是等腰直角三角形,同理△AFM是等腰直角三角形,
∴AM=$\sqrt{2}$AF,AN=$\sqrt{2}$AE,
∵S△AMN=$\frac{1}{2}$AM•AN•sin45°,
S△AEF=$\frac{1}{2}$AE•AF•sin45°,
∴S△AMN:S△AEF=2,
∴S△AMN=2S△AEF,⑤结论错误;
∵点A到MN的距离等于正方形ABCD的边长,
∴S正方形ABCD:S△AMN=$\frac{AB×AB}{\frac{1}{2}×MN×AB}$=2AB:MN,⑥结论正确.
故答案为:⑤.
点评 本题考查了本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和正方形的性质.


科目:初中数学 来源: 题型:选择题
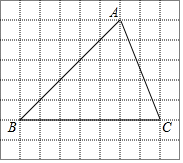 在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )
在正方形网格中,△ABC的位置如图所示,则cos∠B的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com