

���� ��1�����õ��������жϳ���ADE=��CDF����A=��DCB���õ���ADE�ס�CDF�����жϳ���ADC�ס�CDB���ɣ�
��2�������ͣ�1��һ�������õ��������жϳ���ADE=��CDF����A=��DCB���õ���ADE�ס�CDF�����жϳ���ADC�ס�CDB���ɣ�
��3���ɣ�2���Ľ��۵ó���ADE�ס�CDF���жϳ�CF=2AE�����DE�������ù��ɶ�������������ɣ�
��� �⣺��1����m=nʱ������BC=AC��
�ߡ�ACB=90�㣬
���A+��ABC=90�㣬
��CD��AB��
���DCB+��ABC=90�㣬
���A=��DCB��
�ߡ�FDE=��ADC=90�㣬
���FDE-��CDE=��ADC-��CDE��
����ADE=��CDF��
���ADE�ס�CDF��
��$\frac{DE}{DF}=\frac{AD}{DC}$��
�ߡ�A=��DCB����ADC=��BDC=90�㣬
���ADC�ס�CDB��
��$\frac{AD}{DC}=\frac{AC}{BC}$=1��
��$\frac{DE}{DF}$=1
��2���١ߡ�ACB=90�㣬
���A+��ABC=90�㣬
��CD��AB��
���DCB+��ABC=90�㣬
���A=��DCB��
�ߡ�FDE=��ADC=90�㣬
���FDE-��CDE=��ADC-��CDE��
����ADE=��CDF��
���ADE�ס�CDF��
��$\frac{DE}{DF}=\frac{AD}{DC}$��
�ߡ�A=��DCB����ADC=��BDC=90�㣬
���ADC�ס�CDB��
��$\frac{AD}{DC}=\frac{AC}{BC}=\frac{n}{m}$��
��$\frac{DE}{DF}=\frac{n}{m}$
�ڳ�������ͼ��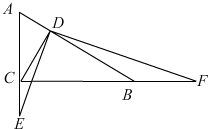
�ߡ�ACB=90�㣬
���A+��ABC=90�㣬
�֡�CD��AB��
���DCB+��ABC=90�㣬
���A=��DCB��
�ߡ�FDE=��ADC=90�㣬
���FDE+��CDE=��ADC+��CDE��
����ADE=��CDF��
���ADE�ס�CDF��
��$\frac{DE}{DF}=\frac{AD}{DC}$��
�ߡ�A=��DCB����ADC=��BDC=90�㣬
���ADC�ס�CDB��
��$\frac{AD}{DC}=\frac{AC}{BC}=\frac{n}{m}$��
��$\frac{DE}{DF}=\frac{n}{m}$��
��3���ɣ�2���У���ADE�ס�CDF��
��$\frac{DE}{DF}=\frac{BC}{AC}$=$\frac{1}{2}$��
��$\frac{AD}{CD}=\frac{AE}{CF}=\frac{DE}{DF}$=$\frac{1}{2}$��
��CF=2AE��
��RtDEF��DE=2$\sqrt{2}$��DF=4$\sqrt{2}$��
��EF=2$\sqrt{10}$��
����Rt��CEF��CF=2AE=2��AC-CE��=2��$\sqrt{5}$-CE����EF=2$\sqrt{10}$��
���ݹ��ɶ����ã�CE2+CF2=EF2��
��CE2+[2��$\sqrt{5}$-CE��]2=40
��CE=2$\sqrt{5}$����CE=-$\frac{2\sqrt{5}}{5}$���ᣩ
����Rt��CEF��CF=2AE=2��AC+CE��=2��$\sqrt{5}$+CE����EF=2$\sqrt{10}$��
���ݹ��ɶ����ã�CE2+CF2=EF2��
��CE2+[2��$\sqrt{5}$+CE��]2=40��
��CE=$\frac{2\sqrt{5}}{5}$����CE=-2$\sqrt{5}$���ᣩ��
����CE=2$\sqrt{5}$��CE=$\frac{2\sqrt{5}}{5}$��
���� �������������ۺ��⣬��Ҫ���������������Ƶ����ʺ��ж������ɶ������ж������ǽⱾ��Ĺؼ�����CE�DZ�����ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | $\frac{5}{2}$ | C�� | $��\frac{5}{2}$ | D�� | ��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��3��4 | B�� | 6��8��9 | C�� | 5��12��13 | D�� | 1��1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com