
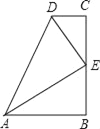
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有( )个.
(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
取AD的中点F,连接EF.根据平行线的性质可证得(1)(4)(5),根据梯形中位线定理可证得(3)正确.根据全等三角形全等的判定可证得(2)的正误,即可得解.
解:如图:取AD的中点F,连接EF.
∵∠B=∠C=90°,
∴AB∥CD;[结论(5)]
∵E是BC的中点,F是AD的中点,
∴EF∥AB∥CD,2EF=AB+CD(梯形中位线定理)①;
∴∠CDE=∠DEF(两直线平等,内错角相等),
∵DE平分∠ADC,
∴∠CDE=∠FDE=∠DEF,
∴DF=EF;
∵F是AD的中点,∴DF=AF,
∴AF=DF=EF②,
由①得AF+DF=AB+CD,即AD=AB+CD;[结论(3)]
由②得∠FAE=∠FEA,
由AB∥EF可得∠EAB=∠FEA,
∴∠FAE=∠EAB,即EA平分∠DAB;[结论(1)]
由结论(1)和DE平分∠ADC,且DC∥AB,可得∠EDA+∠DAE=90°,则∠DEA=90°,即AE⊥DE;[结论(4)].
由以上结论及三角形全等的判定方法,无法证明△EBA≌△DCE.
正确的结论有4个.
故选:C.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
(1)求证:BD=BF;
(2)若AB=10,CD=4,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
(1)图象的另一支位于什么象限?常数n的取值范围是什么?
(2)试比较a、b的大小;
(3)作AC⊥x轴于点C,若△AOC的面积为5,求这个反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与坐标轴分别交于
的图象与坐标轴分别交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象交点为
的图象交点为![]() 、
、![]() ,
,![]() 轴,垂足为
轴,垂足为![]() ,若
,若![]() ,
,![]() ,
,![]() 的面积为
的面积为![]()
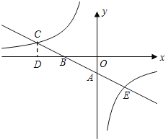
(1)求一次函数与反比例函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
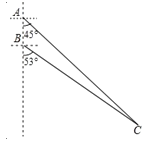
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习片段展示:
【问题】
如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= ,点A的坐标为 .
【操作】
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
【探究】
在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
【应用】结合上面的操作与探究,继续思考:
如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
(1)求A、B两点的坐标;(用含h的式子表示)
(2)当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com