
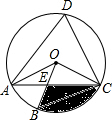
 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.分析 (1)根据四边形ABCD是⊙O的内接四边形得到∠ABC+∠D=180°,根据∠ABC=2∠D得到∠D+2∠D=180°,从而求得∠D=60°,最后根据OA=OC得到∠OAC=∠OCA=30°;
(2)首先根据∠COB=3∠AOB得到∠AOB=30°,从而得到∠COB为直角,然后利用S阴影=S扇形OBC-S△OEC求解.
解答 解:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°;
(2)∵∠COB=3∠AOB,
∴∠AOC=∠AOB+3∠AOB=120°,
∴∠AOB=30°,
∴∠COB=∠AOC-∠AOB=90°,
在Rt△OCE中,OC=2$\sqrt{3}$,
∴OE=OC•tan∠OCE=2$\sqrt{3}$•tan30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
∴S△OEC=$\frac{1}{2}$OE•OC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∴S扇形OBC=$\frac{90π×(2\sqrt{3})^{2}}{360}$=3π,
∴S阴影=S扇形OBC-S△OEC=3π-2$\sqrt{3}$.
点评 本题考查了扇形面积的计算,圆内接四边形的性质,解直角三角形的知识,在求不规则的阴影部分的面积时常常转化为几个规则几何图形的面积的和或差.


科目:初中数学 来源: 题型:解答题
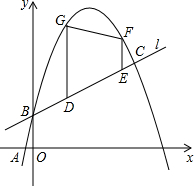 如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).
如图,已知一次函数y1=$\frac{1}{2}$x+b的图象l与二次函数y2=-x2+mx+b的图象l′都经过点B(0,1)和点C,且图象l′过点A(2-$\sqrt{5}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.
如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为$\sqrt{3}$,则AK=2$\sqrt{3}$-3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.694×104人 | B. | 1.694×105人 | C. | 1.694×106人 | D. | 1.694×107人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
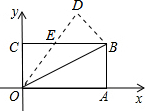 如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )| A. | (4,8) | B. | (5,8) | C. | ($\frac{24}{5}$,$\frac{32}{5}$) | D. | ($\frac{22}{5}$,$\frac{36}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com