
ΓΨΧβΡΩΓΩΘ®ΡΘ–ΆΫ®ΝΔΘ©
(1)»γΆΦ1Θ§Β»―ϋRtΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§CBΘΫCAΘ§÷±œΏEDΨ≠ΙΐΒψCΘ§ΙΐΒψAΉςADΓΆED”ΎΒψDΘ§ΙΐΒψBΉςBEΓΆED”ΎΒψEΘ§«σ÷ΛΘΚΓςBECΓ’ΓςCDAΘΜ

Θ®ΡΘ–Ά”Π”ΟΘ©
Θ®2)»γΆΦ2Θ§“―÷Σ÷±œΏ11ΘΚyΘΫ2xΘΪ3”κx÷αΫΜ”ΎΒψAΓΔ”κy÷αΫΜ”ΎΒψBΘ§ΫΪ÷±œΏ11»ΤΒψAΡφ ±’κ–ΐΉΣ45Γψ÷Ν÷±œΏ12ΘΜ«σ÷±œΏ12ΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®3Θ©»γΆΦ3Θ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒΡΎ”–“ΜΒψBΘ®3Θ§Θ≠4Θ©Θ§ΙΐΒψBΉςBAΓΆx÷α”ΎΒψAΓΔBCΓΆy÷α”ΎΒψCΘ§ΒψP «œΏΕΈAB…œΒΡΕ·ΒψΘ§ΒψD «÷±œΏyΘΫΘ≠2xΘΪ1…œΒΡΕ·Βψ«“‘ΎΒΎΥΡœσœόΡΎΘ° ‘ΧΫΨΩΓςCPDΡήΖώ≥…ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ?»τΡήΘ§«σ≥ωΒψDΒΡΉχ±ξΘ§»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©![]() ;Θ®3Θ©ΡήΘ§ΒψDΒΡΉχ±ξΈΣ
;Θ®3Θ©ΡήΘ§ΒψDΒΡΉχ±ξΈΣ![]() Μρ
Μρ![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”…¥Ι÷±ΒΡΕ®“εΒΟΓœADC=ΓœCEB=90ΓψΘ§ΤΫΫ«ΒΡΕ®“εΚΆΆ§Ϋ«ΒΡ”ύΫ«ΒΡœύΒ»«σ≥ωΓœDAC=ΓœECBΘ§Ϋ«Ϋ«±Ώ÷ΛΟςΓςCDAΓ’ΓςBECΘΜ
Θ®2Θ©÷ΛΟςΓςABOΓ’ΓœBCDΘ§«σ≥ωΒψCΒΡΉχ±ξΈΣΘ®-3Θ§5Θ©Θ§”…ΒψΒΫ÷±œΏ…œΙΙΫ®Εΰ‘Σ“Μ¥ΈΖΫ≥ΧΉι«σ≥ωk=-5Θ§b=-10Θ§¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏl2ΒΡΚ· ΐ±μ¥ο ΫΈΣy=-5x-10ΘΜ
Θ®3Θ©ΙΙΫ®ΓςMCPΓ’ΓςHPDΘ§”…Τδ–‘÷ Θ§ΒψD‘Ύ÷±œΏy=-2x+1«σ≥ωm=![]() Μρn=0Μρ-
Μρn=0Μρ-![]() Θ§ΫΪmΒΡ÷Β¥ζ»κΒψDΉχ±ξΒΟΘ®
Θ§ΫΪmΒΡ÷Β¥ζ»κΒψDΉχ±ξΒΟΘ®![]() Θ§-
Θ§-![]() Θ©ΜρΘ®4Θ§-7Θ©ΜρΘ®
Θ©ΜρΘ®4Θ§-7Θ©ΜρΘ®![]() Θ§-
Θ§-![]() Θ©Θ°
Θ©Θ°
ΫβΘΚΘ®1Θ©»γΆΦΘΚ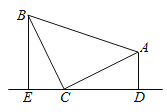
ÿADâEDȧBEâEDȧ
ΓύΓœADC=ΓœCEB=90ΓψΘ§
”÷ΓΏΓœACD+ΓœACB+ΓœBEC=180ΓψΘ§ΓœACB=90ΓψΘ§
ΓύΓœACD+ΓœBEC=90ΓψΘ§
”÷ΓΏΓœACD+ΓœDAC=90ΓψΘ§
ΓύΓœDAC=ΓœECBΘ§
‘ΎΓςCDAΚΆΓςBEC÷–Θ§
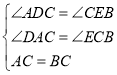
ΓύΓςCDAΓ’ΓςBECΘ®AASΘ©ΘΜ
Θ®2Θ©ΙΐΒψBΉςBCΓΆABΫΜAC”ΎΒψCΘ§CDΓΆy÷αΫΜy÷α
”ΎΒψDΘ§»γΆΦ2Υυ ΨΘΚ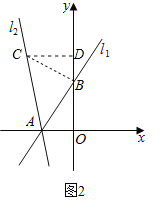
ΓΏCDΓΆy÷αΘ§x÷αΓΆy÷αΘ§
ΓύΓœCDB=ΓœBOA=90ΓψΘ§
”÷ΓΏBCΓΆABΘ§
ΓύΓœABC=90ΓψΘ§
”÷ΓΏΓœABO+ΓœABC+ΓœCBD=180ΓψΘ§
ΓύΓœABO+ΓœCBD=90ΓψΘ§
”÷ΓΏΓœBAO+ΓœABO=90ΓψΘ§
ΓύΓœBAO=ΓœCBDΘ§
”÷ΓΏΓœBAC=45ΓψΘ§
ΓύΓœACB=45ΓψΘ§
ΓύAB=CBΘ§
‘ΎΓςABOΚΆΓœBCD÷–Θ§
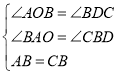
ΓύAO=BDΘ§BO=CDΘ§
”÷ΓΏ÷±œΏl1ΘΚy=2x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§
ΓύΒψAΓΔBΝΫΒψΒΡΉχ±ξΖ÷±πΈΣΘ®![]() Θ§0Θ©Θ§Θ®0Θ§3Θ©Θ§
Θ§0Θ©Θ§Θ®0Θ§3Θ©Θ§
ΓύAO=![]() Θ§BO=3Θ§
Θ§BO=3Θ§
ΓύBD=![]() Θ§CD=3Θ§
Θ§CD=3Θ§
ΓύΒψCΒΡΉχ±ξΈΣΘ®-3Θ§![]() Θ©Θ§
Θ©Θ§
…ηl2ΒΡΚ· ΐ±μ¥ο ΫΈΣy=kx+bΘ®kΓΌ0Θ©Θ§
ΒψAΓΔCΝΫΒψ‘Ύ÷±œΏl2…œΘ§“άΧβ“βΒΟΘΚ
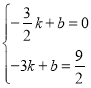 Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ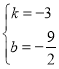
l2ΒΡΚ· ΐ±μ¥ο ΫΈΣ:![]()
Θ®3Θ©Ρή≥…ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§“άΧβ“βΒΟΘ§
ΔΌ»τΒψPΈΣ÷±Ϋ« ±Θ§»γΆΦ3ΦΉΥυ ΨΘΚ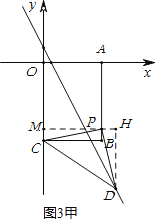
…ηΒψPΒΡΉχ±ξΈΣΘ®3Θ§mΘ©Θ§‘ρPBΒΡ≥ΛΈΣ4+mΘ§
ΓΏΓœCPD=90ΓψΘ§CP=PDΘ§
ΓœCPM+ΓœCDP+ΓœPDH=180ΓψΘ§
ΓύΓœCPM+ΓœPDH=90ΓψΘ§
”÷ΓΏΓœCPM+ΓœDPM=90ΓψΘ§
ΓύΓœPCM=ΓœPDHΘ§
‘ΎΓςMCPΚΆΓςHPD÷–Θ§
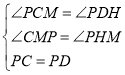
ΓύΓςMCPΓ’ΓςHPDΘ®AASΘ©Θ§
ΓύCM=PHΘ§PM=PDΘ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®7+mΘ§-3+mΘ©Θ§
”÷ΓΏΒψD‘Ύ÷±œΏy=-2x+1…œΘ§
Γύ-2Θ®7+mΘ©+1=-3+mΘ§
ΫβΒΟΘΚ![]()
Φ¥ΒψDΒΡΉχ±ξΈΣ![]()
ΔΎ»τΒψCΈΣ÷±Ϋ« ±Θ§»γΆΦΥυ ΨΘΚ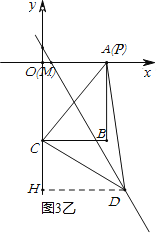
…ηΒψPΒΡΉχ±ξΈΣΘ®3Θ§nΘ©Θ§‘ρPBΒΡ≥ΛΈΣ4+nΘ§
CA=CDȧ
Ά§άμΩ…÷ΛΟςΓςPCMΓ’ΓςCDHΘ®AASΘ©Θ§
ΓύPM=CHΘ§MC=HDΘ§
ΓύΒψDΒΡΉχ±ξΈΣΘ®4+nΘ§-7Θ©Θ§
”÷ΓΏΒψD‘Ύ÷±œΏy=-2x+1…œΘ§
Γύ-2Θ®4+nΘ©+1=-7Θ§
ΫβΒΟΘΚn=0Θ§
ΓύΒψP”κΒψA÷ΊΚœΘ§ΒψM”κΒψO÷ΊΚœΘ§
Φ¥ΒψDΒΡΉχ±ξΈΣΘ®4Θ§-7Θ©ΘΜ
Δέ»τΒψDΈΣ÷±Ϋ« ±Θ§»γΆΦΥυ ΨΘΚ
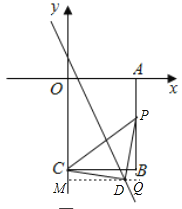
…ηΒψPΒΡΉχ±ξΈΣΘ®3Θ§kΘ©Θ§‘ρPBΒΡ≥ΛΈΣ4+kΘ§
CD=PDȧ
Ά§άμΩ…÷ΛΟςΓςCDMΓ’ΓςPDQΘ®AASΘ©Θ§
ΓύMD=PQΘ§MC=DQΘ§
ΓύΒψDΒΡΉχ±ξΈΣ![]()
”÷ΓΏΒψD‘Ύ÷±œΏy=-2x+1…œΘ§
![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]()
ΓύΒψP”κΒψA÷ΊΚœΘ§ΒψM”κΒψO÷ΊΚœΘ§
Φ¥ΒψDΒΡΉχ±ξΈΣ![]()
ΉέΚœΥυ ωΘ§ΒψDΒΡΉχ±ξΈΣ![]() Μρ
Μρ![]() Μρ
Μρ![]()



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒ»―ϋ÷±Ϋ«![]() ÷–Θ§
÷–Θ§![]() Θ§Βψ
Θ§Βψ![]() ΈΣ
ΈΣ![]() …œ“ΜΒψΘ§Ν§Ϋ”
…œ“ΜΒψΘ§Ν§Ϋ”![]() Θ§“‘
Θ§“‘![]() ΈΣ÷±Ϋ«ΕΞΒψΉωΒ»―ϋ÷±Ϋ«
ΈΣ÷±Ϋ«ΕΞΒψΉωΒ»―ϋ÷±Ϋ«![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§»τ
Θ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡΕ» ΐΈΣΘ® Θ©
ΒΡΕ» ΐΈΣΘ® Θ©

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩAΓΔBΝΫΒΊœύΨύ60kmΘ§ΦΉ¥”AΒΊ»ΞBΒΊΘ§““¥”BΒΊ»ΞAΒΊΘ§ΆΦ÷–![]() ΓΔ
ΓΔ![]() Ζ÷±π±μ ΨΦΉΓΔ““ΝΫ»ΥΒΫBΒΊΒΡΨύάκy(km)”κΦΉ≥ωΖΔ ±Φδx(h)ΒΡΚ· ΐΙΊœΒΆΦœσ.
Ζ÷±π±μ ΨΦΉΓΔ““ΝΫ»ΥΒΫBΒΊΒΡΨύάκy(km)”κΦΉ≥ωΖΔ ±Φδx(h)ΒΡΚ· ΐΙΊœΒΆΦœσ.
(1)ΗυΨίΆΦœσΘ§«σ““ΒΡ–– ΜΥΌΕ».
(2)Ϋβ ΆΫΜΒψAΒΡ ΒΦ “β“ε.
(3)«σΦΉ≥ωΖΔΕύ…Ό ±ΦδΘ§ΝΫ»Υ÷°Φδ«ΓΚΟœύΨύ5kmΘΩ


≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΒΊΦδΒΡ÷±œΏΙΪ¬Ζ≥ΛΈΣ![]() «ßΟΉΘ°“ΜΝΨΫΈ≥ΒΚΆ“ΜΝΨΜθ≥ΒΖ÷±π―ΊΗΟΙΪ¬Ζ¥”ΦΉΓΔ““ΝΫΒΊ“‘ΗςΉ‘ΒΡΥΌΕ»‘»ΥΌœύœρΕχ––Θ§Μθ≥Β±»ΫΈ≥Β‘γ≥ωΖΔ
«ßΟΉΘ°“ΜΝΨΫΈ≥ΒΚΆ“ΜΝΨΜθ≥ΒΖ÷±π―ΊΗΟΙΪ¬Ζ¥”ΦΉΓΔ““ΝΫΒΊ“‘ΗςΉ‘ΒΡΥΌΕ»‘»ΥΌœύœρΕχ––Θ§Μθ≥Β±»ΫΈ≥Β‘γ≥ωΖΔ![]() –Γ ±Θ§ΆΨ÷–ΫΈ≥Β≥ωœ÷ΝΥΙ ’œΘ§ΆΘœ¬Έ§–όΘ§Μθ≥Β»‘ΦΧ–χ–– ΜΘ°
–Γ ±Θ§ΆΨ÷–ΫΈ≥Β≥ωœ÷ΝΥΙ ’œΘ§ΆΘœ¬Έ§–όΘ§Μθ≥Β»‘ΦΧ–χ–– ΜΘ°![]() –Γ ±ΚσΫΈ≥ΒΙ ’œ±Μ≈≈≥ΐΘ§¥Υ ±Ϋ”ΒΫΆ®÷ΣΘ§ΫΈ≥ΒΝΔΩΧΒτΆΖΑ¥‘≠¬Ζ‘≠ΥΌΖΒΜΊΦΉΒΊΘ®Ϋ”ΒΫΆ®÷ΣΦΑΒτΆΖ ±Φδ≤ΜΦΤΘ©Θ°ΉνΚσΝΫ≥ΒΆ§ ±ΒΫ¥οΦΉΒΊΘ§“―÷ΣΝΫ≥ΒΨύΗςΉ‘≥ωΖΔΒΊΒΡΨύάκ
–Γ ±ΚσΫΈ≥ΒΙ ’œ±Μ≈≈≥ΐΘ§¥Υ ±Ϋ”ΒΫΆ®÷ΣΘ§ΫΈ≥ΒΝΔΩΧΒτΆΖΑ¥‘≠¬Ζ‘≠ΥΌΖΒΜΊΦΉΒΊΘ®Ϋ”ΒΫΆ®÷ΣΦΑΒτΆΖ ±Φδ≤ΜΦΤΘ©Θ°ΉνΚσΝΫ≥ΒΆ§ ±ΒΫ¥οΦΉΒΊΘ§“―÷ΣΝΫ≥ΒΨύΗςΉ‘≥ωΖΔΒΊΒΡΨύάκ![]() Θ®«ßΟΉΘ©”κΫΈ≥ΒΥυ”ΟΒΡ ±Φδ
Θ®«ßΟΉΘ©”κΫΈ≥ΒΥυ”ΟΒΡ ±Φδ![]() Θ®–Γ ±Θ©ΒΡΙΊœΒ»γΆΦΥυ ΨΘ§«κΫαΚœΆΦœσΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®–Γ ±Θ©ΒΡΙΊœΒ»γΆΦΥυ ΨΘ§«κΫαΚœΆΦœσΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©Μθ≥ΒΒΡΥΌΕ» «_______«ßΟΉ/–Γ ±ΘΜΫΈ≥ΒΒΡΥΌΕ» «_______«ßΟΉ/–Γ ±ΘΜ![]() ÷ΒΈΣ_______Θ°
÷ΒΈΣ_______Θ°
Θ®2Θ©«σΫΈ≥ΒΨύΤδ≥ωΖΔΒΊΒΡΨύάκ![]() Θ®«ßΟΉΘ©”κΥυ”Ο ±Φδ
Θ®«ßΟΉΘ©”κΥυ”Ο ±Φδ![]() Θ®–Γ ±Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ Ϋ≤Δ–¥≥ωΉ‘±δΝΩ
Θ®–Γ ±Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ Ϋ≤Δ–¥≥ωΉ‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©«κ÷±Ϋ”–¥≥ωΜθ≥Β≥ωΖΔΕύ≥Λ ±ΦδΝΫ≥ΒœύΨύ![]() «ßΟΉΘ°
«ßΟΉΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΝ–ΖΫ≥ΧΉιΫβ”Π”ΟΧβΡ≥–ΘΉι÷·ΓΑ¥σ ÷ά≠–Γ ÷Θ§“ε¬τœΉΑ°–ΡΓ±ΜνΕ·Θ§ΦΤΜ°ΙΚ¬ρΚΎΓΔΑΉΝΫ÷÷―’…ΪΒΡΈΡΜ·…άΫχ–– ÷Μφ…ηΦΤΚσ≥ω έΘ§≤ΔΫΪΥυΜώάϊ»σ»Ϊ≤ΩΨηΗχ…Ϋ«χάßΡ―ΚΔΉ”Θ°“―÷ΣΗΟ―ß–Θ¥”≈ζΖΔ –≥ΓΜ®2400‘ΣΙΚ¬ρΝΥΚΎΓΔΑΉΝΫ÷÷―’…ΪΒΡΈΡΜ·…ά100ΦΰΘ§ΟΩΦΰΈΡΜ·…άΒΡ≈ζΖΔΦέΦΑ ÷ΜφΚσΒΡΝψ έΦέ»γ±μΘΚ
≈ζΖΔΦέΘ®‘Σ) | Νψ έΦέΘ®‘Σ) | |
ΚΎ…ΪΈΡΜ·…ά | 25 | 45 |
ΑΉ…ΪΈΡΜ·…ά | 20 | 35 |
(1)―ß–ΘΙΚΫχΚΎΓΔΑΉΈΡΜ·…άΗςΦΗΦΰ?
(2)Ά®Ιΐ ÷Μφ…ηΦΤΚσ»Ϊ≤Ω έ≥ωΘ§«σΗΟ–Θ’β¥Έ“ε¬τΜνΕ·ΥυΜώάϊ»σΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΒΡΉχ±ξ.
ΒΡΉχ±ξ.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΒψP «Νβ–ΈABCD±Ώ…œΒΡ“ΜΕ·ΒψΘ§Υϋ¥”ΒψA≥ωΖΔ―Ί‘ΎAΓζBΓζCΓζD¬ΖΨΕ‘»ΥΌ‘ΥΕ·ΒΫΒψDΘ§…ηΓςPADΒΡΟφΜΐΈΣyΘ§PΒψΒΡ‘ΥΕ· ±ΦδΈΣxΘ§‘ρyΙΊ”ΎxΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ®ΓΓΓΓΘ©

A.  B.
B.  C.
C.  D.
D. 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ»‘ΡΕΝœ¬Οφ“ΜΕΈ≤ΡΝœΘ§‘ΌΆξ≥…ΚσΟφΒΡΈ ΧβΘΚ
≤ΡΝœΘΚΙΐ≈ΉΈοœΏy=ax2Θ®aΘΨ0Θ©ΒΡΕ‘≥Τ÷α…œ“ΜΒψΘ®0Θ§©¹![]() Θ©ΉςΕ‘≥Τ÷αΒΡ¥ΙœΏlΘ§‘ρ≈ΉΈοœΏ…œ»Έ“β“ΜΒψPΒΫΒψFΘ®0Θ§
Θ©ΉςΕ‘≥Τ÷αΒΡ¥ΙœΏlΘ§‘ρ≈ΉΈοœΏ…œ»Έ“β“ΜΒψPΒΫΒψFΘ®0Θ§![]() Θ©ΒΡΨύάκ”κPΒΫlΒΡΨύάκ“ΜΕ®œύΒ»Θ§Έ“Ο«ΫΪΒψF”κ÷±œΏlΖ÷±π≥ΤΉς’β≈ΉΈοœΏΒΡΫΙΒψΚΆΉΦœΏΘ§»γy=x2ΒΡΫΙΒψΈΣΘ®0Θ§
Θ©ΒΡΨύάκ”κPΒΫlΒΡΨύάκ“ΜΕ®œύΒ»Θ§Έ“Ο«ΫΪΒψF”κ÷±œΏlΖ÷±π≥ΤΉς’β≈ΉΈοœΏΒΡΫΙΒψΚΆΉΦœΏΘ§»γy=x2ΒΡΫΙΒψΈΣΘ®0Θ§![]() Θ©Θ°
Θ©Θ°
Έ ΧβΘΚ»τ÷±œΏy=kx+bΫΜ≈ΉΈοœΏy=![]() x2”ΎAΓΔBΓΔACΓΔBD¥Ι÷±”Ύ≈ΉΈοœΏΒΡΉΦœΏlΘ§¥Ι÷±ΉψΖ÷±πΈΣCΓΔDΘ®»γΆΦΘ©Θ°
x2”ΎAΓΔBΓΔACΓΔBD¥Ι÷±”Ύ≈ΉΈοœΏΒΡΉΦœΏlΘ§¥Ι÷±ΉψΖ÷±πΈΣCΓΔDΘ®»γΆΦΘ©Θ°
ΔΌ«σ≈ΉΈοœΏy=![]() x2ΒΡΫΙΒψFΒΡΉχ±ξΘΜ
x2ΒΡΫΙΒψFΒΡΉχ±ξΘΜ
ΔΎ«σ÷ΛΘΚ÷±œΏABΙΐΫΙΒψ ±Θ§CFΓΆDFΘΜ
ΔέΒ±÷±œΏABΙΐΒψΘ®©¹1Θ§0Θ©Θ§«““‘œΏΕΈABΈΣ÷±ΨΕΒΡ‘≤”κΉΦœΏlœύ«– ±Θ§«σ’βΧθ÷±œΏΕ‘”ΠΒΡΚ· ΐΫβΈω ΫΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏΒΡΕΞΒψΈΣPΘ®©¹3Θ§3Θ©Θ§”κy÷αΫΜ”ΎΒψAΘ®0Θ§4Θ©Θ§»τΤΫ“ΤΗΟ≈ΉΈοœΏ ΙΤδΕΞΒψP―Ί÷±œΏ“ΤΕ·ΒΫΒψPΓδΘ®3Θ§©¹3Θ©Θ§ΒψAΒΡΕ‘”ΠΒψΈΣAΓδΘ§‘ρ≈ΉΈοœΏ…œPAΕΈ…®ΙΐΒΡ«χ”ρΘ®“θ”Α≤ΩΖ÷Θ©ΒΡΟφΜΐΈΣΘ®ΓΓΓΓΘ©

A. 24 B. 12 C. 6 D. 4![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com