
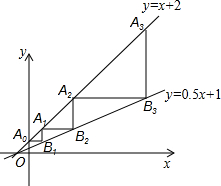
 如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.
如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n. 分析 根据两直线的解析式分别求出A0、A1、A2…An-1与B1、B2、…Bn的坐标,然后将A0B1、A1B2、A2B3、A3B4的长度求出,然后根据规律写出An-1Bn的长即可.
解答 解:令x=0代入y=x+2,
∴y=2,
∴A0(0,2),
令y=2代入y=0.5x+1,
∴x=2,
∴A0B1=2,
令x=2代入y=x+2,
∴y=4,
∴A1(2,4),
∴令y=4代入y=0.5x+1,
∴x=6,
∴B2(6,4),
∴A1B2=4,
同理可求得:A2B3=8,A3B4=16,
由以上规律可知:An-1Bn=2n,
故答案为:2n
点评 本题考查数字规律问题,解题的关键根据一次函数解析式求出相关点的坐标,然后找出An-1Bn的长的规律,本题属于中等题型.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )
如图,当刻度尺的一边与⊙O相切时,另一边与⊙O的两个交点处的读数如图所示(单位:cm),圆的半径是5,那么刻度尺的宽度为( )| A. | $\frac{25}{6}$cm | B. | 4cm | C. | 3cm | D. | 2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 第1个 | 第2个 | 第3个 | 第4个 | … |
| $\sqrt{{1^2}+1}$ | $\sqrt{{2^2}+2}$ | $\sqrt{{3^2}+3}$ | $\sqrt{{4^2}+4}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )
一个表面标有汉字的多面体的平面展开图如图所示,如果“你”在上面,“乐”在前面,则不正确的是( )| A. | “年”在下面 | B. | “祝”在后面 | C. | “新”在左边 | D. | “快”在左边 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0>m1>m2 | B. | 0>m2>m1 | C. | m2>m1>0 | D. | m1>m2>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com