
如图所示,E、C分别是AB、AD上的两点,BC与DE相交于点O,且有AE·AB=AC·AD,则OD∶OB=OC∶OE成立吗?并说明理由.

|
解:OD∶OB=OC∶OE成立,理由是: 由AE·AB=AC·AD,得 又因为∠A=∠A 所以△ABC∽△ADE,所以∠B=∠D 又因为∠BOE=∠DOC,所以△BOE∽△DOC 所以OB∶OD=OE∶OC 即OD∶OB=OC∶OE成立. 说明:欲判断OD∶OB=OC∶OE是否成立,应观察四条线段所在的△BOE与△DOC是否相似,由对顶角相等,故∠BOE=∠DOC,只要再看∠B与∠D是否相等即可判断出两三角形是否相似,由已知条件较容易推出△ABC∽△ADE,故∠B=∠D,问题得解.可见,第一次推证出△ABC∽△ADE的目的是为第二次推证△BOE∽△DOC创造条件,这种方法要逐步掌握. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
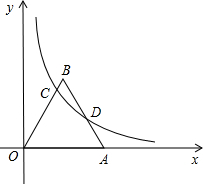 分别交AB、OB于D、C两点,其中D为AB中点
分别交AB、OB于D、C两点,其中D为AB中点查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图所示,这个风铃分别由正三、正四、正五、正六、正八、正十和正十二边形的饰物组成,共重144克,(假设绳子和横杆的重量为0),请你计算出每个正多边形饰物的重量.
15、如图所示,这个风铃分别由正三、正四、正五、正六、正八、正十和正十二边形的饰物组成,共重144克,(假设绳子和横杆的重量为0),请你计算出每个正多边形饰物的重量.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•石景山区二模)如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳3×2-2=4步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为
(2012•石景山区二模)如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳3×2-2=4步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com