已知一个等腰三角形的腰长为5厘米，底边长4厘米，求出顶角余弦的值（试用两种不同的方法解）．
分析：解法一：过A点作AD⊥BC，足为D，将三角形分为两个直角三角形，先求∠B的度数，再利用三角形内角和定理求∠A，最后求cosA；
解法二：过A点作AD⊥BC，垂足为D，过C点作CE⊥AB，垂足为E，用勾股定理求AD，用面积法求CE，再用勾股定理求AE，利用∠A的余弦定义求解．
解答：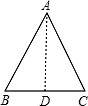
解：解法一：如图，
AB=AC=5，BC=4，过A点作AD⊥BC，垂足为D，
cosB=
=
，∴B≈65°，A=180°-2B=50°，
∴cosA≈0.68；
解法二：如图，AB=AC=5，BC=4，过A点作AD⊥BC，垂足为D，
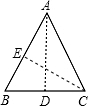
过C点作CE⊥AB，垂足为E，
由勾股定理，得AD=
=
，
由面积法可知，CE•AB=AD•BC，
∴CE=
，由勾股定理，得AE=
=
，
∴cosA=
=
=0.68．
点评：本题考查了锐角三角函数值的求法．关键是把问题转化到直角三角形中求角的度数，或者直接根据定义求解．
