
【题目】如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
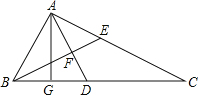
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EFEC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
【答案】(1)见解析;(2)见解析;(3)AE=![]() .
.
【解析】
(1)首先证明∠EBC=∠C,∠ABD=∠ADB,再根据∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,可得结论.
(2)证明△AEF∽△BEA可得结论.
(3)设BE交AG于J,连接DJ,DE.证明四边形AJDE是平行四边形,推出DE⊥BC,AE=DJ,想办法求出DJ即可解决问题.
(1)证明:∵EB=EC,
∴∠EBC=∠C,
∵AG⊥BD,BG=GD,
∴AB=AD,
∴∠ABD=∠ADB,
∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,
∴∠ABE=∠DAC,
即∠ABE=∠EAF;
(2)证明:∵∠AEF=∠BEA,∠EAF=∠ABE,
∴△AEF∽△BEA,
∴![]() ,
,
∴AE2=EFEB,
∵EB=EC,
∴AE2=EFEC;
(3)解:设BE交AG于J,连接DJ,DE.
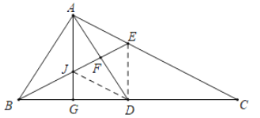
∵AG垂直平分线段BD,
∴JB=JD,
∴∠JBD=∠JDG,
∵∠JBD=∠C,
∴∠JDB=∠C,
∴DJ∥AC,
∴∠AEF=∠DJF,
∵AD=2AF,
∴AF=DF,
在△AFE和△DFJ中,
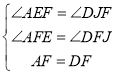 ,
,
∴△AFE≌△DFJ(AAS),
∴EF=FJ,AE=DJ,
∵AF=DF,
∴四边形AJDE是平行四边形,
∴DE∥AG,
∵AG⊥BC,
∴ED⊥BC,
∵EB=EC,
∴BD=DC=![]() ,
,
∴BG=DG=![]() ,
,
∵tan∠JDG=tan∠C=![]() ,
,
∴JG=![]() ,
,
∵∠JGD=90°,
∴DJ= ,
,
∴AE=DJ=![]() .
.


科目:初中数学 来源: 题型:
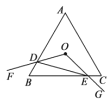
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
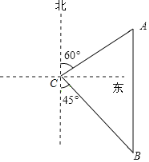
【题目】如图,一艘轮船从位于灯塔![]() 的北偏东60°方向,距离灯塔60海里的小岛
的北偏东60°方向,距离灯塔60海里的小岛![]() 出发,沿正南方向航行一段时间后,到达位于灯塔
出发,沿正南方向航行一段时间后,到达位于灯塔![]() 的南偏东45°方向上的
的南偏东45°方向上的![]() 处,这时轮船
处,这时轮船![]() 与小岛
与小岛![]() 的距离是__________海里.
的距离是__________海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁5辆客车前往宁波东站接员工返岗.已知现有A、B两种客车,A型客车的载客量为45人/辆,每辆租金为400元;B型客车的载客量为30人/辆,每辆租金为280元.设租用A型客车为x辆,所需费用为y元.
(1)求y关于x的函数解析式;
(2)若该企业需要接的员工有205人,请求出租车费用最小值,并写出对应的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点A,B在x轴的负半轴上,反比例函数y=![]() (k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,
(k1≠0)在第二象限内的图象经过正方形ABCD的顶点D(m,2)和BC边上的点G(n,![]() ),直线y=k2x+b(k2≠0)经过点D,点G,则不等式
),直线y=k2x+b(k2≠0)经过点D,点G,则不等式![]() ≤k2x+b的解集为__________.
≤k2x+b的解集为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
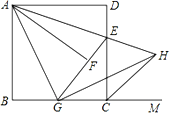
【题目】如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
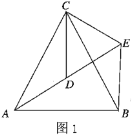
如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ;
;
探究发现
(1)善思组发现:![]() ,请你帮他们写出推理过程;
,请你帮他们写出推理过程;
(2)钻研组受善思组的启发,求出了![]() 度数,请直接写出
度数,请直接写出![]() 等于______度;
等于______度;
(3)奋进组在前面两组的基础上又探索出了![]() 与
与![]() 的位置关系为______(请直接写出结果);
的位置关系为______(请直接写出结果);
拓展探究
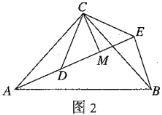
(4)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() ,试探究
,试探究![]() ,
,![]() ,
,![]() 之间有怎样的数量关系.
之间有怎样的数量关系.
创新组类比善思组的发现,很快证出![]() ,进而得出
,进而得出![]() .请你写出
.请你写出![]() ,
,![]() ,
,![]() 之间的数量关系并帮创新组完成后续的证明过程.
之间的数量关系并帮创新组完成后续的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A,B(1,0),与
与x轴交于点A,B(1,0),与![]() 轴交于点C(0,3),对称轴为直线
轴交于点C(0,3),对称轴为直线![]() .
.
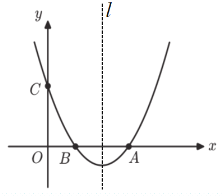
(1)求抛物线的解析式及点A的坐标;
(2)在对称轴![]() 上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
(3)若点P是抛物线上一动点,从点C沿抛物线向点A运动,过点P作PD//![]() 轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com