
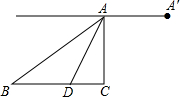
 如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30$\sqrt{3}$m到达A′处,
如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30$\sqrt{3}$m到达A′处,分析 (1)解直角三角形即可得到结论;
(2)过A′作A′E⊥BC交BC的延长线于E,连接A′D,于是得到A′E=AC=60,CE=AA′=30$\sqrt{3}$,在Rt△ABC中,求得DC=$\frac{\sqrt{3}}{3}$AC=20$\sqrt{3}$,然后根据三角函数的定义即可得到结论.
解答 解:(1)由题意得:∠ABD=30°,∠ADC=60°,
在Rt△ABC中,AC=60m,
∴AB=$\frac{AC}{sin30°}$=$\frac{60}{\frac{1}{2}}$=120(m);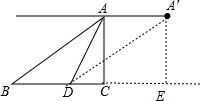
(2)过A′作A′E⊥BC交BC的延长线于E,连接A′D,
则A′E=AC=60,CE=AA′=30$\sqrt{3}$,
在Rt△ABC中,AC=60m,∠ADC=60°,
∴DC=$\frac{\sqrt{3}}{3}$AC=20$\sqrt{3}$,
∴DE=50$\sqrt{3}$,
∴tan∠AA′D=tan∠A′DC=$\frac{A′E}{DE}$=$\frac{60}{50\sqrt{3}}$=$\frac{2}{5}$$\sqrt{3}$.
答:从无人机A′上看目标D的俯角的正切值是$\frac{2}{5}$$\sqrt{3}$.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助俯角构造直角三角形并解直角三角形.注意方程思想与数形结合思想的应用.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.59×104 | B. | 659×104 | C. | 65.9×105 | D. | 6.59×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2=4.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com