
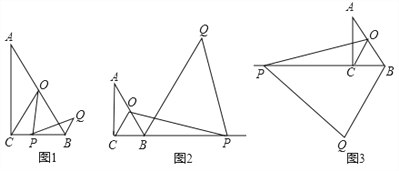
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)如图3,当点P在BC延长线上时,若∠BPO=15°,BP=4,请求出BQ的长.
【答案】(1)BQ=CP;(2)成立:PC=BQ;(3)![]() .
.
【解析】
试题(1)结论:BQ=CP.如图1中,作PH∥AB交CO于H,可得△PCH是等边三角形,只要证明△POH≌△QPB即可;
(2)成立:PC=BQ.作PH∥AB交CO的延长线于H.证明方法类似(1);
(3)如图3中,作CE⊥OP于E,在PE上取一点F,使得FP=FC,连接CF.设CE=CO=a,则FC=FP=2a,EF=![]() a,在Rt△PCE中,表示出PC,根据PC+CB=4,可得方程
a,在Rt△PCE中,表示出PC,根据PC+CB=4,可得方程![]() ,求出a即可解决问题;
,求出a即可解决问题;
试题解析:解:(1)结论:BQ=CP.
理由:如图1中,作PH∥AB交CO于H.
在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,∴CO=AO=BO,∠CBO=60°,∴△CBO是等边三角形,∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,∴∠CHP=∠CPH=60°,∴△CPH是等边三角形,∴PC=PH=CH,∴OH=PB,∵∠OPB=∠OPQ+∠QPB=∠OCB+∠COP,∵∠OPQ=∠OCP=60°,∴∠POH=∠QPB,∵PO=PQ,∴△POH≌△QPB,∴PH=QB,∴PC=BQ.
(2)成立:PC=BQ.理由:作PH∥AB交CO的延长线于H.
在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,∴CO=AO=BO,∠CBO=60°,∴△CBO是等边三角形,∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,∴∠CHP=∠CPH=60°,∴△CPH是等边三角形,∴PC=PH=CH,∴OH=PB,∵∠POH=60°+∠CPO,∠QPO=60°+∠CPQ,∴∠POH=∠QPB,∵PO=PQ,∴△POH≌△QPB,∴PH=QB,∴PC=BQ.
(3)如图3中,作CE⊥OP于E,在PE上取一点F,使得FP=FC,连接CF.
∵∠OPC=15°,∠OCB=∠OCP+∠POC,∴∠POC=45°,∴CE=EO,设CE=CO=a,则FC=FP=2a,EF=![]() a,在Rt△PCE中,PC=
a,在Rt△PCE中,PC=![]() =
=![]() =
=![]() ,∵PC+CB=4,∴
,∵PC+CB=4,∴![]() ,解得a=
,解得a=![]() ,∴PC=
,∴PC=![]() ,由(2)可知BQ=PC,∴BQ=
,由(2)可知BQ=PC,∴BQ=![]() .
.



科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
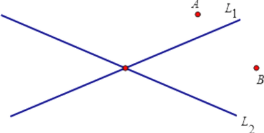
【题目】如图,A、B是两个工厂,L1、L2是两条公路,现要在这一地区建一加油站,要求加油站到A、B两厂的路程相等,且到两条路的距离相等,请用尺规作图找出符合条件的点P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
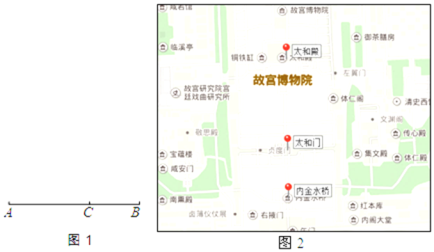
【题目】如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BCAB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在“附中博识课程中”,小白菜们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的宏伟.太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
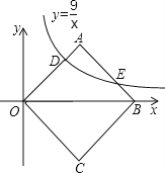
【题目】如图,Rt△AOB中,∠OAB=90°,OA=AB,将Rt△AOB放置于直角坐标系中,OB在x轴上,点O是原点,点A在第一象限.点A与点C关于x轴对称,连结BC,OC.双曲线![]() (x>0)与OA边交于点D、与AB边交于点E.
(x>0)与OA边交于点D、与AB边交于点E.
(1)求点D的坐标;
(2)求证:四边形ABCD是正方形;
(3)连结AC交OB于点H,过点E作EG⊥AC于点G,交OA边于点F,求四边形OHGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向240km的O处,以每小时30km的速度向南偏东60°的OB方向移动,距台风中心150km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到台风的影响,求出受台风影响的时间有多长?
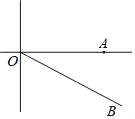
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:对于一个关于![]() 的一元二次方程
的一元二次方程![]() (其中a≠0,a、b、c为常数)的两根分别为
(其中a≠0,a、b、c为常数)的两根分别为![]() ,
,![]() ,我们有如下发现①若
,我们有如下发现①若![]() ,
,![]() 为整数,则这个一元二次方程的判别式
为整数,则这个一元二次方程的判别式![]() 一定为完全平方数;②
一定为完全平方数;② ![]() ,
,![]() 满足韦达定理:即
满足韦达定理:即![]() ,
,![]() ;
;
③韦达定理也有逆定理,即如果两数![]() 和
和![]() 满足如下关系:
满足如下关系:![]() ,
,![]() ,那么这两个数
,那么这两个数![]() 和
和![]() 是方程
是方程![]() (
(![]() )的两个根.
)的两个根.
请应用上述材料解决以下问题:
(1)若实数![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,
的两个根,
①当![]() 时,则
时,则![]() ,
,![]() ;
;
②若![]() 均为整数且
均为整数且![]() ,求
,求![]() 的值;
的值;
(2)已知实数![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com