
分析 (1)①证明四边形DPEC为平行四边形可得结论;
②根据四边形内角和为360°,列等式求出x+y的值;
(2)根据P、D、E位置的不同,分五种情况:①y-x=m+n,如图2,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
②x-y=m-n,如图3,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
③x+y=m+n,如图4,点P在线段BA上时,根据四边形的内角和为360°列等式,化简后得出结论;
④x-y=m+n,如图5,同理得出结论;
⑤y-x=m-n,如图6,同理得出结论.
解答 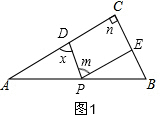 解:(1)①如图1,∵PD∥BC,PE∥AC,
解:(1)①如图1,∵PD∥BC,PE∥AC,
∴四边形DPEC为平行四边形,
∴∠DPE=∠C,
∵∠DPE=m,∠C=n=90°,
∴m=90°;
②∵∠ADP=x,∠PEB=y,
∴∠CDP=180°-x,∠CEP=180°-y,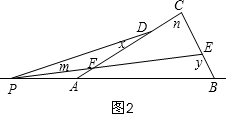
∵∠C+∠CDP+∠DPE+∠CEP=360°,
∠C=90°,∠DPE=50°,
∴90°+180°-x+50°+180°-y=360°,
∴x+y=140°;
(2)分五种情况:
①y-x=m+n,如图2, 理由是:
理由是:
∵∠DFP=n+∠FEC,∠FEC=180°-y,
∴∠DFP=n+180°-y,
∵x+m+∠DFP=180°,
∴x+m+n+180°-y=180°,
∴y-x=m+n;
②x-y=m-n,如图3,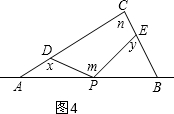 理由是:
理由是:
同理得:m+180°-x=n+180°-y,
∴x-y=m-n;
③x+y=m+n,如图4,理由是:
由四边形内角和为360°得:180°-x+m+180°-y+n=360°,
∴x+y=m+n;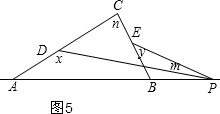
④x-y=m+n,如图5,理由是:
同理得:180°=m+n+y+180°-x,
∴x-y=m+n;
⑤y-x=m-n,如图6,理由是:
同理得:n+180°-x=m+180°-y,
∴y-x=m-n.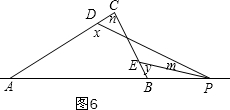
点评 本题是三角形的综合题,难度不大,考查了平行四边形的性质和判定及三角形的内角和、外角定理,熟练掌握三角形的内角和为180°及三角形的一个外角等于与它不相邻的两个内角的和;能根据动点位置的不同准确列出各角之间的关系式并化简即可.


科目:初中数学 来源: 题型:解答题
 如图是某学校主楼梯从底楼到二楼的楼梯截面图,已知BC=7米,AB=6+3$\sqrt{3}$米,中间平台DE与地面AB平行,且DE的长度为2米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°,楼梯宽度为3米.
如图是某学校主楼梯从底楼到二楼的楼梯截面图,已知BC=7米,AB=6+3$\sqrt{3}$米,中间平台DE与地面AB平行,且DE的长度为2米,DM、EN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°,楼梯宽度为3米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某人带自产的土豆进城出售,他先按市场价售出一些后,发现天色较晚,决定降价出售.为了方便顾客,他的钱包中有一些备用零钱用于找零.学习小组观察发现售出土豆数量x与他钱包中的总钱数y的关系如图所示.结合图象回答下列问题:
某人带自产的土豆进城出售,他先按市场价售出一些后,发现天色较晚,决定降价出售.为了方便顾客,他的钱包中有一些备用零钱用于找零.学习小组观察发现售出土豆数量x与他钱包中的总钱数y的关系如图所示.结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com