
分析 将三角形数变形,总结规律找出第n个数,即可求出第1008个三角形数与第1006个三角形数的差.
解答 解:三角形数变形得:1=1,3=1+2,6=1+2+3,10=1+2+3+4,…,
第n个数为1+2+3+…+n=$\frac{1}{2}$n(1+n),
∴第1008个数为$\frac{1}{2}$×1008×1009=508536,第1006个数为$\frac{1}{2}$×1006×1007=506521,
∴508536-506521=2015,
∴第1008个数与第1006个数的差是2015,
故答案为:2015.
点评 本题主要考查数字的变化规律问题,根据数列得出第n个数为1+2+3+…+n=$\frac{1}{2}$n(1+n)是解题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
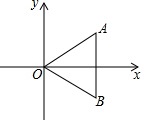 如图,△ABO关于x轴对称,若点A的坐标为(3,1),则点B的坐标为( )
如图,△ABO关于x轴对称,若点A的坐标为(3,1),则点B的坐标为( )| A. | (1,3) | B. | (-1,3) | C. | (3,-1) | D. | (-1,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
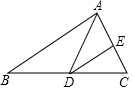 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC交BC于点D,点E是边AC上一点,连接DE,若∠ADE=40°,求证:DE∥AB.
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC交BC于点D,点E是边AC上一点,连接DE,若∠ADE=40°,求证:DE∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com