
(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
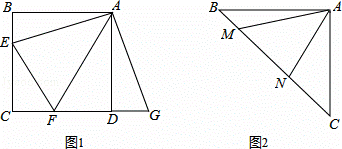


(1)证明:在正方形ABCD中,
∴∠ABE=∠ADG,AD=AB,
在△ABE和△ADG中,
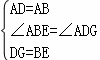
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∴∠EAG=90°,
在△FAE和△GAF中,
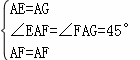 ,
,
∴△FAE≌△GAF(SAS),
∴EF=FG
(2)解:如图2,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.
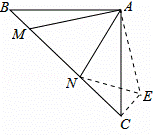
∵AB=AC,∠BAC=90°,∴∠B=∠C=45°.
∵CE⊥BC,∴∠ACE=∠B=45°.
在△ABM和△ACE中,
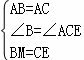
∴△ABM≌△ACE(SAS).
∴AM=AE,∠BAM=∠CAE.
∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.
于是,由∠BAM=∠CAE,得∠MAN=∠EAN=45°.
在△MAN和△EAN中,
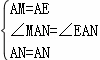
∴△MAN≌△EAN(SAS).
∴MN=EN.
在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.
∴MN2=BM2+NC2.
∵BM=1,CN=3,
∴MN2=12+32,
∴MN=




科目:初中数学 来源: 题型:
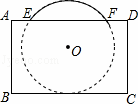
把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
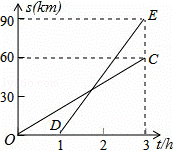
已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?


查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件中,必然事件是
A. 抛掷一枚硬币,正面朝上
B. 打开电视,正在播放广告
C. 体育课上,小刚跑完1000米所用时间为1分钟
D. 袋中只有4个球,且都是红球,任意摸出一球是红球


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com