
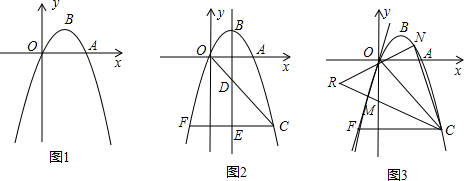
分析 (1)先解方程ax(x-2)=0得到则A(2,0),则利用对称性得到B点的横坐标为1,再利用顶点B在直线y=x上得到B(1,1),然后把B点坐标代入y=ax(x-2)中求出a即可;
(2)抛物线解析式为y=-x2+2x,直线x=1交x轴于K,如图2,设C(t,-t2+2t),则E(1,-t2+2t),利用线段中点坐标公式得到D(1,$\frac{-{t}^{2}+2t+1}{2}$),再证明△OKD∽△CED,然后利用相似比得到关于t的方程,再解方程求出t即可得到C点坐标;
(3)作NQ⊥CF于Q,MP⊥CF于P,CF交y轴于点H,如图3,先求出F点坐标得到CF=4,FH=1,OH=3,设N(m,-m2+2m),则E(1,-m2+2m),则NQ=-m2+2m+3,再证明△CNQ≌△MCP得到CP=NQ=-m2+2m+3,CQ=MP=3-m,所以FP=CF-PC=m2-2m+1,接着证明△FPM∽△FHO,然后利用相似得到方程(3-m):3=(m2-2m+1):1,再解方程求出m即可得到N点坐标.
解答  解:(1)当y=0时,ax(x-2)=0,解得x1=0,x2=2,则A(2,0),
解:(1)当y=0时,ax(x-2)=0,解得x1=0,x2=2,则A(2,0),
所以抛物线的对称轴为直线x=1,即B点的横坐标为1,
而顶点B在直线y=x上;
所以B(1,1),
把B(1,1)代入y=ax(x-2)得a=-1;
(2)抛物线解析式为y=-x2+2x,直线x=1交x轴于K,如图2,
设C(t,-t2+2t),则E(1,-t2+2t),
∵BD=DE,即D点为BE的中点,
∴D(1,$\frac{-{t}^{2}+2t+1}{2}$),
∴KD=$\frac{{t}^{2}-2t-1}{2}$,DE=$\frac{-{t}^{2}+2t+1}{2}$-(-t2+2t)=$\frac{{t}^{2}-2t+1}{2}$,
∵OK∥CE,
∴△OKD∽△CED,
∴OK:CE=DK:DE,即1:(t-1)=$\frac{{t}^{2}-2t-1}{2}$:$\frac{{t}^{2}-2t+1}{2}$,
解得t1=0(舍去),t2=3,
∴C(3,-3);
(3)作NQ⊥CF于Q,MP⊥CF于P,CF交y轴于点H,如图3,
∵点C(3,-3)与点F关于直线x=1对称,
∴F(-1,-3),
∴CF=4,FH=1,OH=3,
设N(m,-m2+2m),则E(1,-m2+2m),则NQ=-m2+2m+3,
∵NR=NC,
∴∠NRC=∠NCR,
∴∠NCR=$\frac{1}{2}$(180°-∠CNR),
而∠CNR=4∠FCM,
∴∠NCR=90°-2∠FCM,
∵∠NCR=90°-∠CNQ-∠FCM,
∴90°-2∠FCM=90°-∠CNQ-∠FCM,
∴∠FCM=∠CNQ,
在△CNQ和△MCP中
$\left\{\begin{array}{l}{∠CQN=∠MPC}\\{∠CNQ=∠MCP}\\{NC=CM}\end{array}\right.$,
∴△CNQ≌△MCP,
∴CP=NQ=-m2+2m+3,CQ=MP=3-m,
∴FP=CF-PC=4-(-m2+2m+3)=m2-2m+1,
∵MP∥OH,
∴△FPM∽△FHO,
∴MP:OH=FP:FH,即(3-m):3=(m2-2m+1):1,
解得m=$\frac{5}{3}$,
∴N点坐标为($\frac{5}{3}$,$\frac{5}{9}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,记住线段的中点坐标公式;会利用全等三角形的知识证明线段相等和相似比计算线段的长.


科目:初中数学 来源: 题型:选择题
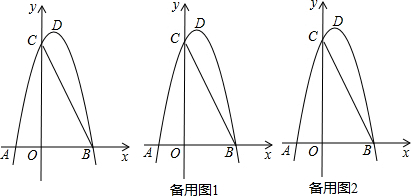
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )
如图,△A1B1A2,△A2B2A3,△A3B3A4,…△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA2=1,则OA2016的长为( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
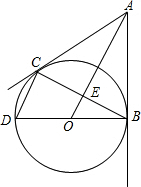 如图,AB,AC分别切⊙O于B,C,⊙O的直径BD=6,连接CD,AO,BC.AO与BC相交于点E.
如图,AB,AC分别切⊙O于B,C,⊙O的直径BD=6,连接CD,AO,BC.AO与BC相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
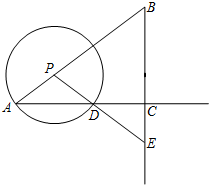 如图,在Rt△ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,设PA=x.
如图,在Rt△ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,设PA=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
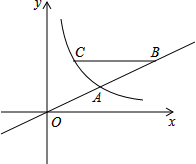 如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=$\frac{1}{2}$x相交于横坐标为2的点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com