
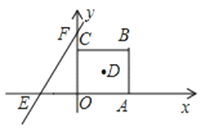
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı߳�Ϊa��ֱ��y=bx+c��x����E����y����F����a��b��c�ֱ�����![]() ��
��![]()
��1����ֱ��y=bx+c�Ľ���ʽ��ֱ��д��������OABC�ĶԽ��ߵĽ���D�����ꣻ
��2��ֱ��y=bx+c��x����������ÿ���ƶ�1����λ���ȵ��ٶ�ƽ�ƣ���ƽ�Ƶ�ʱ��Ϊt�룬���Ƿ����t��ֵ��ʹֱ��EFƽ��������OABC������������ڣ������t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=2x��8����D��2,2������2�����ڣ�t=5
��������
��1������ƽ���ķǸ��ԡ����θ�ʽ������������������a��b��c��ֵ���Ӷ����ֱ�߽���ʽ��Ȼ�������B�����꣬�����е����깫ʽ���������D�����ꣻ
��2���������E�����꣬Ȼ���������ɵã���ֱ��ƽ��������OABC�����ʱ��ƽ�ƺ��ֱ�߹���D��Ȼ�����ƽ�ƺ��ֱ�߽���ʽ���Ӷ����ƽ�ƺ�ֱ����x��Ľ������꣬���ɵó����ۣ�
�⣺��1����![]() ��
��![]() ����
����![]()
��![]() ��
��![]()
��ã�a=4��b=2��![]()
��ֱ��EF�Ľ���ʽΪy=2x��8�������εı߳�Ϊ4
���B��������4,4��
�ߵ�DΪ������OABC�ĶԽ��ߵĽ���
���DΪOB���е�
���D��������![]() ��=��2,2��
��=��2,2��
��2�����ڣ�
��y=0����y=2x��8�У���ã�x=-4
���E��������-4,0��
��ƽ�ƺ�Ľ���ʽΪy=2x��m
��ƽ�ƺ��ֱ��ƽ��������OABC�������
��ƽ�ƺ��ֱ�߹���D
����D���������y=2x��m����
2=2��2��m
��ã�m=-2
��ƽ�ƺ�Ľ���ʽΪy=2x��2
��y=0����y=2x��2�����x=1
��ƽ�ƺ���x��Ľ�������Ϊ��1,0����ƽ�ƾ���Ϊ1����-4��=5����λ����
��ƽ��ʱ��t=5��1=5�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019���й����������ղ�������4��28�����ڱ���������¡�ؿ�Ļ��������������Ϊ����ɫ��������������Կ�����������ӭ������������οͽ��ιۣ���ͳ�ƣ�����һС����ǰ��������ο;��ܼ�Լ32.7���˴Σ������й���Ҳ�Ƿdz��ܻ�ӭ�ij��ݣ��ݵ��飬�й���5��1����������ԼΪ4���ˣ�5��3����������ԼΪ9���ˣ���5��1�յ�5��3���ο�����������������ͬ�����й����������ο���������ƽ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ѷ���(3x+2)(x-3)=2x-6����Ϊһ����ʽ����д�����Ķ�����ϵ����һ����ϵ���ͳ����
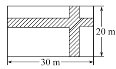
��2���ڿ�Ϊ20m����Ϊ30m�ľ��ε�����������ͬ�����ĵ�·�����²�����Ϊ���أ������������Ҫ551m2��������·��ӦΪ���٣���ֻ�з��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC��BD���ڵ�O������O��ֱ�߷ֱ�BC��AD��F��E����AD=6cm��AB=4cm��OE=2cm��������EFCD���ܳ��ǣ� ��
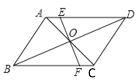
A.16cmB.15cmC.14cmD.12cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��F�ֱ�ΪAD��CD���е㣬BF��CE�ཻ�ڵ�H��ֱ��EN��CB���ӳ����ڵ�N����CM��EN�ڵ�M����BF�ڵ�G����CM=CD�������½��ۣ���BF��CE����ED=EM����tan��ENC=![]() ����S�ı���DEHF=4S��CHF��������ȷ���۵ĸ���Ϊ����
����S�ı���DEHF=4S��CHF��������ȷ���۵ĸ���Ϊ����
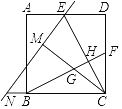
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߲�Ʒ�ĸ���ֵ��ij��˾�ƻ����з�������1200���²�Ʒ���о��ӹ�����Ͷ���г������мס��������������߱��ӹ���������˾�ɳ������Ա�ֱ������������˽���������������Ϣ��
��Ϣһ�����������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ����10�죻
��Ϣ�����ҹ���ÿ��ӹ��������Ǽ���ÿ��ӹ�������1.5����
����������Ϣ����ס�����������ÿ��ֱ��ܼӹ����ټ��²�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� x ��һԪ���η��̣�x��1����x��2��=m��m+1��
��1����֤�������� m ȡ��ֵ�˷�����������ʵ������
��2����ԭ���̵����� x1��x 2 ����![]() ���� m ��ֵ��
���� m ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
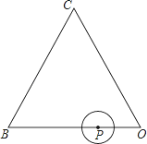
����Ŀ����ͼ���ȱ�������OBC�ı߳�Ϊ10����P��O��B��C��O�ķ����˶�����P�İ뾶Ϊ![]() �� ��P�˶�һȦ���OBC�ı�����________�Σ�ÿ������ʱ����P���ȱ������ζ������������________��
�� ��P�˶�һȦ���OBC�ı�����________�Σ�ÿ������ʱ����P���ȱ������ζ������������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����н�����̣�
 =
= =
=![]() =
=![]() -2��
-2��
 =
= =
=![]() ��
��
��ش��������⣺
��1���۲�����Ľ�����̣���ֱ��д��ʽ��![]() =�� ����
=�� ����
��2���۲�����Ľ�����̣���ֱ��д��ʽ��![]() =�� ����
=�� ����
��3�������������ṩ�Ľⷨ������![]() +������+
+������+![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com