
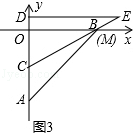
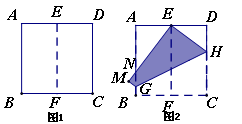
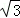 ��ֱ�DZ�CD��y���ϣ��ҵ�C���A�غϣ�Rt��CDE��y��������ƽ���ƶ�������C�˶�����Oʱֹͣ�˶�������������⣺
��ֱ�DZ�CD��y���ϣ��ҵ�C���A�غϣ�Rt��CDE��y��������ƽ���ƶ�������C�˶�����Oʱֹͣ�˶�������������⣺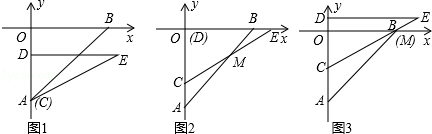
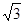 ��
��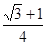 h2+4h+8��
h2+4h+8��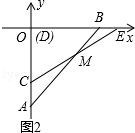
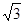 ��
��
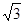 ��
�� ��
��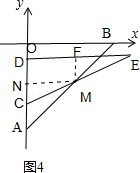
 ��AC=h��AN=NM��
��AC=h��AN=NM��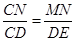 ��
��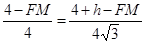 ��
��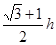 ��
��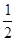 ��4��4
��4��4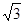 ��
��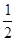 ��4
��4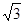 4��h������4��
4��h������4��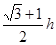 ��=��
��=��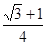 h2+4h+8��
h2+4h+8��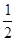 OC��OB=
OC��OB=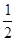 ��6��h����6=18��3h��
��6��h����6=18��3h��

 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
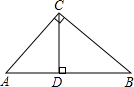
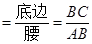 .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ġ����������ǵ����Զ��壬���������⣺��ͼ�ڣ���֪sinA
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ġ����������ǵ����Զ��壬���������⣺��ͼ�ڣ���֪sinA �����С�AΪ��ǣ�����sadA��ֵ��
�����С�AΪ��ǣ�����sadA��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����
����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com